题目内容
已知函数 ,数列
,数列 满足
满足 ,且
,且 .
.
(1)试探究数列 是否是等比数列?
是否是等比数列?
(2)试证明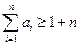 ;
;
(3)设 ,试探究数列
,试探究数列 是否存在最大项和最小项?若存在求出
是否存在最大项和最小项?若存在求出
最大项和最小项,若不存在,说明理由.
解:(1)由 得
得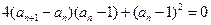
 ∴
∴ 或
或 ---
---
∵ ,∴
,∴ 不合舍去-------
不合舍去-------
由 得
得 方法1:由
方法1:由 得
得
∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列--
的等比数列--
〔方法2:由 得
得 当
当 时
时 ∴
∴
( )∴数列
)∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列〕
的等比数列〕
(2)证明:由(1)知数列 是首项为
是首项为 ,公比为
,公比为 的等比数列
的等比数列
∴ ,∴
,∴ -----------
-----------
∴ =
= --
--
∵对 有
有 ,∴
,∴ ∴
∴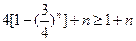 ,即
,即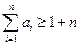 --
--
(3)由 得
得
∴ =
= ------------
------------
令 ,则
,则 ,
, =
=
∵函数 在
在 上为增函数,在
上为增函数,在 上为减函数-------
上为减函数-------
当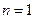 时
时 ,当
,当 时
时 ,当
,当 时,
时, ,当
,当 时
时 ,
,
∵
 ,且
,且
∴当 时,
时, 有最小值,即数列
有最小值,即数列 有最小项,
有最小项,
最小项为 ------
------
当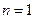 即
即 时,
时, 有最大值,即数列
有最大值,即数列 有最大项,
有最大项,
最大项为 .
.
解析

练习册系列答案
相关题目
 ,数列{
,数列{ }满足
}满足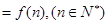 ,且{
,且{ 的取值范围是 ( )
的取值范围是 ( ) B.
B. 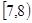 C.
C.  D.
D. 
 ,数列
,数列 满足
满足 ,
,
 ;
;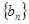 满足
满足 …+
…+ ,求
,求
 ,数列
,数列 满足
满足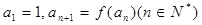
 求数列
求数列 ,求
,求 .
. ,数列
,数列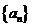 满足
满足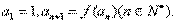
 ,求
,求 .
. ,数列
,数列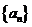 满足
满足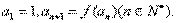
 ,求
,求 .
.