题目内容
 如图,已知四棱锥S-ABCD的底面ABCD是边长为1的正方形,SA⊥平面ABCD,SA=2,E是侧棱SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是边长为1的正方形,SA⊥平面ABCD,SA=2,E是侧棱SC上的一点.(1)求证:平面EBD⊥平面SAC;
(2)求四棱锥S-ABCD的体积.
分析:(1)由SA⊥平面ABCD,BD?平面ABCD,知SA⊥BD,由底面ABCD为正方形,知BD⊥AC,由此能够证明面EBD⊥面SAC.
(2)由底面ABCD为边长为1的正方形,SA⊥平面ABCD,SA=2,能求出四棱锥S-ABCD的体积.
(2)由底面ABCD为边长为1的正方形,SA⊥平面ABCD,SA=2,能求出四棱锥S-ABCD的体积.
解答: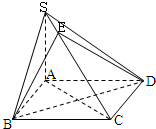 解:(1)∵SA⊥平面ABCD,BD?平面ABCD,
解:(1)∵SA⊥平面ABCD,BD?平面ABCD,
∴SA⊥BD,
∵底面ABCD为正方形,
∴BD⊥AC,
∵SA∩AC=A,
∴BD⊥平面SAC,
∵BD?平面EBD,
∴面EBD⊥面SAC.
(2)∵底面ABCD为边长为1的正方形,
SA⊥平面ABCD,SA=2,
∴VS-ABCD=
×1×1×2=
.
 解:(1)∵SA⊥平面ABCD,BD?平面ABCD,
解:(1)∵SA⊥平面ABCD,BD?平面ABCD,∴SA⊥BD,
∵底面ABCD为正方形,
∴BD⊥AC,
∵SA∩AC=A,
∴BD⊥平面SAC,
∵BD?平面EBD,
∴面EBD⊥面SAC.
(2)∵底面ABCD为边长为1的正方形,
SA⊥平面ABCD,SA=2,
∴VS-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查平面与平面垂直的证明,考查四棱锥的体积的求法,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
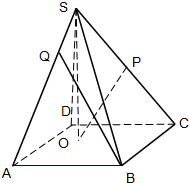 如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
如图,已知四棱锥S-ABCD的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,SO的长为3,O到AB,AD的距离分别为2和1,P是SC的中点.
 (2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.
(2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点. (2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.
(2010•江西模拟)(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形S'SC.