题目内容
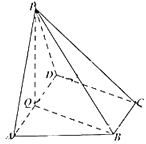
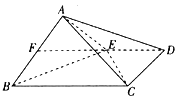
【题目】如图,圆台O1O2的轴截面为等腰梯形A1A2B2B1,A1A2![]() B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
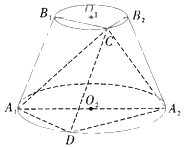
(1)求证:A1C⊥A2C;
(2)若∠B1B2C=60°,则当三棱锥C﹣A1DA2的体积取最大值时,求A1D与平面CA1A2所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)设圆O1,O2的半径分别为r,2r,由题意可得r=1,则![]() ,
,![]() ,
,![]() ,连接O1O2,O1C,O2C,可得O1O2⊥O1C,由此可证结论;
,连接O1O2,O1C,O2C,可得O1O2⊥O1C,由此可证结论;
(2)由题意可求得点D为弧A1A2的中点时,V有最大值![]() ,连接DO2,以点O2为坐标原点,以O2D,O2A2,O2O1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,利用空间向量即可求得线面角.
,连接DO2,以点O2为坐标原点,以O2D,O2A2,O2O1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,利用空间向量即可求得线面角.
(1)证:设圆O1,O2的半径分别为r,2r,
∵圆台的侧面积为6π,
∴![]() ,解得r=1,
,解得r=1,
∴在等腰梯形A1A2B2B1中,![]() ,
,
连接O1O2,O1C,O2C,在圆台O1O2中,O1O2⊥平面B1CB2,O1C在平面B1CB2内,
∴O1O2⊥O1C,
又O1C=1,故在△O1CO2中,CO2=2,
在△CA1A2中,![]() ,故∠A1CA2=90°,即A1C⊥A2C;
,故∠A1CA2=90°,即A1C⊥A2C;
(2)解:由题意可知,三棱锥C﹣A1DA2的体积为![]() ,
,
又在Rt△A1DA2中,![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
即点D为弧A1A2的中点时,V有最大值![]() ,
,
连接DO2,∵O1O2⊥平面A1DA2,DO2⊥O2A2,
∴以点O2为坐标原点,以O2D,O2A2,O2O1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
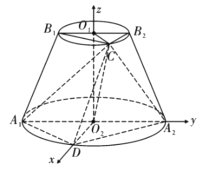
则A1(0,﹣2,0),A2(0,2,0),D(2,0,0),由∠B1B2C=60°,可知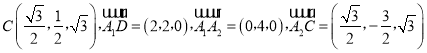 ,
,
设平面CA1A2的一个法向量为![]() ,则
,则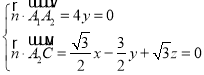 ,可取
,可取![]() ,
,
∴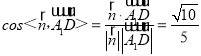 ,
,
∴A1D与平面CA1A2所成角的正弦值为![]() .
.

【题目】2014年,中央和国务院办公厅印发《关于引导农村土地经营权有序流转发展农业适度规模经营的意见》,要求大力发展土地流转和适度规模经营.某种粮大户2015年开始承包了一地区的大规模水田种植水稻,购买了一种水稻收割机若干台,这种水稻收割机随着使用年限的增加,每年的养护费也相应增加,这批水稻收割机自购买使用之日起,5年以来平均每台水稻收割机的养护费用数据统计如下:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
养护费用 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
(1)从这5年中随机抽取2年,求平均每台水稻收割机每年的养护费用至少有1年多于2万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)若该水稻收割机的购买价格是每台16万元,由(2)中的回归方程,从每台水稻收割机的年平均费用角度,你认为一台该水稻收割机是使用满5年就淘汰,还是继续使用到满8年再淘汰?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: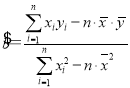 ,
,![]()
![]() .
.