题目内容
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线(A,B为切点),则四边形PACB面积的最小值( )A.
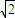
B.2

C.2
D.4
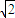
【答案】分析:由圆C的标准方程可得圆心为(1,1),半径为1,由于四边形PACB面积等于 2× PA×AC=PA,而PA=
PA×AC=PA,而PA=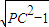 ,
,
故当PC最小时,四边形PACB面积最小,又PC的最小值等于圆心C到直线l的距离d,求出d 即可得到四边形PACB面积的最小值.
解答:解:圆C:x2+y2-2x-2y+1=0 即 (x-1)2+(y-1)2=1,表示以C(1,1)为圆心,以1为半径的圆.
由于四边形PACB面积等于 2× PA×AC=PA,而 PA=
PA×AC=PA,而 PA=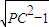 ,
,
故当PC最小时,四边形PACB面积最小.
又PC的最小值等于圆心C到直线l:3x+4y+8=0 的距离d,而d=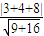 =3,
=3,
故四边形PACB面积的最小的最小值为 =2
=2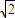 ,
,
故选B.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,判断故当PC最小时,四边形PACB面积最小,是解题的关键.
 PA×AC=PA,而PA=
PA×AC=PA,而PA=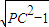 ,
,故当PC最小时,四边形PACB面积最小,又PC的最小值等于圆心C到直线l的距离d,求出d 即可得到四边形PACB面积的最小值.
解答:解:圆C:x2+y2-2x-2y+1=0 即 (x-1)2+(y-1)2=1,表示以C(1,1)为圆心,以1为半径的圆.
由于四边形PACB面积等于 2×
 PA×AC=PA,而 PA=
PA×AC=PA,而 PA=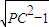 ,
,故当PC最小时,四边形PACB面积最小.
又PC的最小值等于圆心C到直线l:3x+4y+8=0 的距离d,而d=
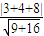 =3,
=3,故四边形PACB面积的最小的最小值为
 =2
=2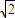 ,
,故选B.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,判断故当PC最小时,四边形PACB面积最小,是解题的关键.

练习册系列答案
相关题目