题目内容
在半径为3的球内有一内接正三棱锥,它的底面三个顶点恰好同在一个大圆上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路程为
- A.12π
- B.14π
- C.5π
- D.7π
D
分析:球面上两点之间最短的路径是大圆(圆心为球心)的劣弧的弧长,因此最短的路径分别是经过的各段弧长的和.
解答:由题意可知,球面上两点之间最短的路径是大圆(圆心为球心)的劣弧的弧长,
内接正三棱锥,它的底面三个顶点恰好同在一个大圆上,一个动点从三棱锥的
一个顶点出发沿球面运动,经过其余三点后返回,
则经过的最短路程为:一个半圆一个 圆,即:
圆,即: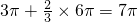
故选D.
点评:本题考查球的内接多面体,球面距离,考查空间想象能力,是基础题.
分析:球面上两点之间最短的路径是大圆(圆心为球心)的劣弧的弧长,因此最短的路径分别是经过的各段弧长的和.
解答:由题意可知,球面上两点之间最短的路径是大圆(圆心为球心)的劣弧的弧长,
内接正三棱锥,它的底面三个顶点恰好同在一个大圆上,一个动点从三棱锥的
一个顶点出发沿球面运动,经过其余三点后返回,
则经过的最短路程为:一个半圆一个
 圆,即:
圆,即: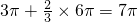
故选D.
点评:本题考查球的内接多面体,球面距离,考查空间想象能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目