题目内容
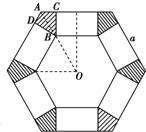 如图,把边长为a的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖直六棱柱的盒子(不计接缝),要使所做成的盒子体积最大,问如何裁剪?
如图,把边长为a的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖直六棱柱的盒子(不计接缝),要使所做成的盒子体积最大,问如何裁剪?
分析:由图形设BO长为x,可求出AB,在直角三角形ABD中解三角形算出BD的长,即求出六棱柱的高的关于x的表达式,再求出底面的用x表示的面积表达式,用体积公式就可以得到六棱柱的体积表达式,再利用函数的单调性判断出函数取到最值时x的值即可.
解答:解:设原正六边形中剪去六个角中的其中一个为ADBC,连接AO(O为正六边形的外接圆的圆心),又设BO长为x,则直六棱柱的盒子的体积为
V(x)=6×
x2(a-x)×
=(a-x)x2=
(ax2-x3),
∴V′(x)=
(2ax-3x2),
令V′(x)=
(2ax-3x2)=0,得x=
a,x=0(舍),
因为V(x)只有一个极值,所以它是最大值,
即x=
a时,[V(x)]max=
,
因此,只要连接AO,在AO上取AB长为
,再过点B作BC垂直于正六边形的边长于点C,BD垂直于正六边形的边长于点D,剪去四边形ADBC,同样可剪去另外五角,则折成无盖直六棱柱的盒子体积最大.
V(x)=6×
| ||
| 4 |
| ||
| 2 |
| 9 |
| 4 |
∴V′(x)=
| 9 |
| 4 |
令V′(x)=
| 9 |
| 4 |
| 2 |
| 3 |
因为V(x)只有一个极值,所以它是最大值,
即x=
| 2 |
| 3 |
| a3 |
| 3 |
因此,只要连接AO,在AO上取AB长为
| a |
| 3 |
点评:考查直六棱柱的体积公式,及用公式将几何问题转化为函数最值的能力,用导数证明函数的单调性求出最值及最值取到时自变量的求法.

练习册系列答案
相关题目
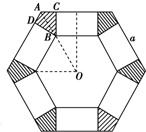 如图,把边长为a的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖直六棱柱的盒子(不计接缝),要使所做成的盒子体积最大,问如何裁剪?
如图,把边长为a的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖直六棱柱的盒子(不计接缝),要使所做成的盒子体积最大,问如何裁剪?
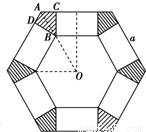
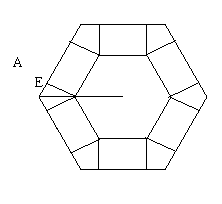 (2)当
(2)当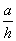 为多少时,体积V最大,最大值是多少?
为多少时,体积V最大,最大值是多少?