题目内容
某企业为适应市场需求,准备投入资金16万元生产W和R型两种产品.经市场预测,生产W型产品所获利润yW(万元)与投入资金xW(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5 万元.生产R型产品所获利润yR(万元)与投入资金xR(万元)满足关系yR=| 1 |
| 2 |
| xR |
分析:若设生产R型产品投入资金为x万元,则生产W型产品投入资金为(16-x)万元,所获总利润y=
(16-x)+
,其中x∈[0,16],通过换元,令
=t,则y=-
t2+
t+4=-
(t-1)2+
;容易求得y的最大值以及对应的x的值.
| 1.5 |
| 6 |
| 1 |
| 2 |
| x |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 17 |
| 4 |
解答:解:设生产R型产品投入资金为x万元,则生产W型产品的投入资金为(16-x)万元,所获总利润为y万元.
则由题意,得:y=
(16-x)+
,x∈[0,16]
令
=t,则y=-
t2+
t+4=-
(t-1)2+
所以t=1,即x=12=1时,y取最大值ymax=
(万元)
此时,16-x=15(万元)
所以,生产W型产品投入资金15万元,R型产品投入1万元时,获得最大总利润,是
万元.
则由题意,得:y=
| 1 |
| 4 |
| 1 |
| 2 |
| x |
令
| x |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 17 |
| 4 |
所以t=1,即x=12=1时,y取最大值ymax=
| 17 |
| 4 |
此时,16-x=15(万元)
所以,生产W型产品投入资金15万元,R型产品投入1万元时,获得最大总利润,是
| 17 |
| 4 |
点评:本题通过换元法,考查了二次函数模型的应用,并且利用二次函数的性质求其最值问题,是基础题.

练习册系列答案
相关题目
 (万元)与投入资金
(万元)与投入资金 (万元)成正比例关系,且当投入资金为6万元时,可获利润1.5
(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5 万元。生产R型产品所获利润
万元。生产R型产品所获利润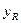 (万元)与投入资金
(万元)与投入资金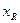 (
( 万元)满足关系
万元)满足关系 ,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少? ,为获得最大利润,问生产W,R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元)
,为获得最大利润,问生产W,R型两种产品各应投入资金多少万元?获得的最大利润是多少?(精确到0.01万元)