题目内容
已知函数![]()
(1)设![]() ,当m≥
,当m≥![]() 时,求g(x)在[
时,求g(x)在[![]() ]上的最大值;
]上的最大值;
(2)若![]() 上是单调减函数,求实数m的取值范围.
上是单调减函数,求实数m的取值范围.
(1) m≥![]() 时,g(x)max=2m-
时,g(x)max=2m-![]() ; (2) -1≤m<9.
; (2) -1≤m<9.
解析:
(1)g(x)= .
.
即m≥![]() 时,g′(x)≤0,g(x)在[
时,g′(x)≤0,g(x)在[![]() ,2]上单调递减,
,2]上单调递减,
∴g(x)max=g(![]() )=2m-
)=2m-![]() -ln2.
-ln2.
所以m≥![]() 时,g(x)max=2m-
时,g(x)max=2m-![]() ;
;
(2)因为函数y=log![]() [8-f(x)]在[1,+∞)上是单调减函数,则其导数在[1,+∞)上恒小于等于零.
[8-f(x)]在[1,+∞)上是单调减函数,则其导数在[1,+∞)上恒小于等于零.
所以
![]() 恒成立.
恒成立.
因为log![]() e<0,所以
e<0,所以![]() 在[1,+∞)恒成立.即
在[1,+∞)恒成立.即![]() 在[1,+∞)恒成立.
在[1,+∞)恒成立.
因为 在[1,+∞)上不恒成立,所以
在[1,+∞)上不恒成立,所以 在[1,+∞)上恒成立.
在[1,+∞)上恒成立.
得 在[1,+∞)上恒成立. 所以-1≤m<9.
在[1,+∞)上恒成立. 所以-1≤m<9.
(本题也可用复合函数进行处理)

练习册系列答案
相关题目
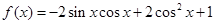
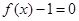 在(0,
在(0,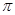 )内有两个零点
)内有两个零点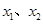 ,求
,求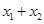 的值;
的值;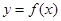 的图像向左移动
的图像向左移动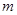
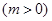 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于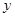 轴对称,求
轴对称,求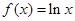 ,
,
 (其中
(其中 是
是 的导函数),求
的导函数),求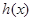 的最大值;
的最大值;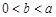 时,求证:
时,求证: ;
;  ,当
,当 时,不等式
时,不等式 恒成立,求
恒成立,求 的最大值
的最大值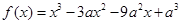 .
.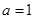 ,求函数
,求函数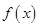 的极值;
的极值;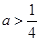 ,且当
,且当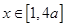 时,
时,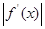
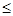 12a恒成立,试确定
12a恒成立,试确定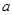 的取值范围.
的取值范围.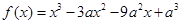 .
.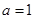 ,求函数
,求函数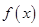 的极值;
的极值;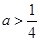 ,且当
,且当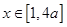 时,
时,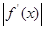
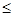 12a恒成立,试确定
12a恒成立,试确定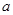 的取值范围.
的取值范围.