题目内容
已知0＜a＜1，则函数y=ax和y=（a-1）x2在同坐标系中的图象只能是图中的
- A.
- B.
- C.
- D.
D
分析：利用底数的范围判断指数函数的单调性，利用二次项的正负来判断抛物线的开口方向，得答案．
解答：∵0＜a＜1，∴y=ax是减函数，∵0＜a＜1，∴a-1＜0，∴y=（a-1）x2开口向下，
故选D．
点评：本题考查了指数函数和二次函数的图象，是在同一坐标系统中，有相同的参数，解析式中的参数决定函数的什么性质，特殊点．
分析：利用底数的范围判断指数函数的单调性，利用二次项的正负来判断抛物线的开口方向，得答案．
解答：∵0＜a＜1，∴y=ax是减函数，∵0＜a＜1，∴a-1＜0，∴y=（a-1）x2开口向下，
故选D．
点评：本题考查了指数函数和二次函数的图象，是在同一坐标系统中，有相同的参数，解析式中的参数决定函数的什么性质，特殊点．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
已知函数f（x）的定义域为（0，+∞），若y=
在（0，+∞）上为增函数，则称f（x）为“一阶比增函数”；若y=
在（0，+∞）上为增函数，则称f（x）为“二阶比增函数”．我们把所有“一阶比增函数”组成的集合记为Ω1，所有“二阶比增函数”组成的集合记为Ω2．
（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
求证：d（2d+t-4）＞0；
（Ⅲ）定义集合Φ={f（x）|f（x）∈Ω2，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数M，使得?f（x）∈Φ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．
在（0，+∞）上为增函数，则称f（x）为“一阶比增函数”；若y=在（0，+∞）上为增函数，则称f（x）为“二阶比增函数”．我们把所有“一阶比增函数”组成的集合记为Ω1，所有“二阶比增函数”组成的集合记为Ω2．（Ⅰ）已知函数f（x）=x3-2hx2-hx，若f（x）∈Ω1，且f（x）∉Ω2，求实数h的取值范围；
（Ⅱ）已知0＜a＜b＜c，f（x）∈Ω1且f（x）的部分函数值由下表给出，
| x | a | b | c | a+b+c |
| f（x） | d | d | t | 4 |
（Ⅲ）定义集合Φ={f（x）|f（x）∈Ω2，且存在常数k，使得任取x∈（0，+∞），f（x）＜k}，请问：是否存在常数M，使得?f（x）∈Φ，?x∈（0，+∞），有f（x）＜M成立？若存在，求出M的最小值；若不存在，说明理由．
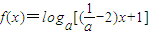在区间上[1，3]的函数值大于0恒成立，则实数a的取值范围是（ ）
