题目内容
集合A是由适合以下性质的函数f(x)构成的:对于任意的,且u、υ∈(-1,1),都有|f(u)-f(υ)|≤3|u-υ|.
(1)判断函数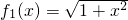 是否在集合A中?并说明理由;
是否在集合A中?并说明理由;
(2)设函数f(x)=ax2+bx,且f(x)∈A,试求2a+b的取值范围;
(3)在(2)的条件下,若f(2)=6,且对于满足(2)的每个实数a,存在最小的实数m,使得当x∈[m,2]时,|f(x)|≤6恒成立,试求用a表示m的表达式.
解:(1)f1(x)∈A,任取u、υ∈(-1,1),且u≠υ,
则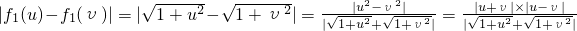
因为|u|< ,|υ|<
,|υ|<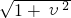 ,且|u+υ|≤|u|+|υ|
,且|u+υ|≤|u|+|υ|
所以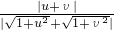 <1
<1
所以|f1(u)-f1(υ)|<|u-υ|<3|u-υ|,亦即f1(x)∈A
(2)因为f(x)=ax2+bx属于集合A,所以,任取u、υ∈(-1,1)且u≠υ,
则3|u-υ|≥|f(u)-f(υ)|=|(u-υ)(au+aυ+b)|,
也即|au+aυ+b|≤3 ①
设t=u+υ,则上式化为|at+b|≤3②
因为u,υ∈(-1,1),所以-2<t<2
①式对任意的u,υ∈(-1,1)恒成立,即②式对t∈(-2,2)恒成立可以证明|2a|+|b|≤3,所以|2a+b|≤3,
即2a+b∈[-3,3]
(3)由f(2)=6可知2a+b=3
又由(2)可知-3≤2a+b≤3,所以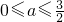 ,
,
当a=0时,b=3,f(x)=3x在[m,2]上为单调递增函数,f(m)=3m,f(2)=4
令3m=-6,可得m=-2
当a>0时,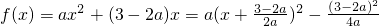 .
.
此时,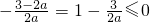 ,且当x∈R时f(x)的最小值为
,且当x∈R时f(x)的最小值为
若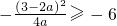 ,即
,即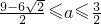 时,m为方程f(x)=6的较小根,所以
时,m为方程f(x)=6的较小根,所以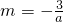
若 <-6,即0<a<
<-6,即0<a< 时,由于f(x)在
时,由于f(x)在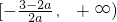 上单调递增,
上单调递增,
所以m为方程f(x)=-6的较大根,所以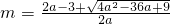 ,
,
综上可知,m=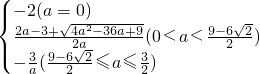
分析:(1)先取u、υ∈(-1,1)时,检验|f1(u)-f1(υ)|≤3|u-υ|是否成立,根据已知给出判断即可
(2)由f(x)∈A可得,|u-υ|≥|f(u)-f(υ)|=|(u-υ)(au+aυ+b)|,即|au+aυ+b|≤3 成立,设t=u+υ,结合u,υ∈(-1,1)可得t的范围,可求
(3)由f(2)=6可得,2a+b=3由(2)中2a+b的范围,可求a的范围,而当x∈[m,2]时,结合二次函数的性质可求x∈R时f(x)min,通过与函数的最小值与端点6,与-6的大小可的m与方程的根的关系,从而可求a与m之间的关系
点评:本题以集合的关系为载体主要考查了函数的单调性于函数的值域的求解,而函数的恒成立的问题的解决常转化为求解函数的最值.
则
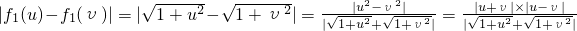
因为|u|<
 ,|υ|<
,|υ|<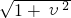 ,且|u+υ|≤|u|+|υ|
,且|u+υ|≤|u|+|υ|所以
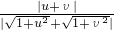 <1
<1所以|f1(u)-f1(υ)|<|u-υ|<3|u-υ|,亦即f1(x)∈A
(2)因为f(x)=ax2+bx属于集合A,所以,任取u、υ∈(-1,1)且u≠υ,
则3|u-υ|≥|f(u)-f(υ)|=|(u-υ)(au+aυ+b)|,
也即|au+aυ+b|≤3 ①
设t=u+υ,则上式化为|at+b|≤3②
因为u,υ∈(-1,1),所以-2<t<2
①式对任意的u,υ∈(-1,1)恒成立,即②式对t∈(-2,2)恒成立可以证明|2a|+|b|≤3,所以|2a+b|≤3,
即2a+b∈[-3,3]
(3)由f(2)=6可知2a+b=3
又由(2)可知-3≤2a+b≤3,所以
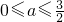 ,
,当a=0时,b=3,f(x)=3x在[m,2]上为单调递增函数,f(m)=3m,f(2)=4
令3m=-6,可得m=-2
当a>0时,
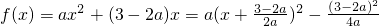 .
.此时,
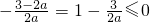 ,且当x∈R时f(x)的最小值为
,且当x∈R时f(x)的最小值为
若
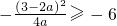 ,即
,即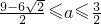 时,m为方程f(x)=6的较小根,所以
时,m为方程f(x)=6的较小根,所以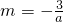
若
 <-6,即0<a<
<-6,即0<a< 时,由于f(x)在
时,由于f(x)在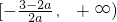 上单调递增,
上单调递增,所以m为方程f(x)=-6的较大根,所以
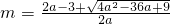 ,
,综上可知,m=
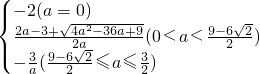
分析:(1)先取u、υ∈(-1,1)时,检验|f1(u)-f1(υ)|≤3|u-υ|是否成立,根据已知给出判断即可
(2)由f(x)∈A可得,|u-υ|≥|f(u)-f(υ)|=|(u-υ)(au+aυ+b)|,即|au+aυ+b|≤3 成立,设t=u+υ,结合u,υ∈(-1,1)可得t的范围,可求
(3)由f(2)=6可得,2a+b=3由(2)中2a+b的范围,可求a的范围,而当x∈[m,2]时,结合二次函数的性质可求x∈R时f(x)min,通过与函数的最小值与端点6,与-6的大小可的m与方程的根的关系,从而可求a与m之间的关系
点评:本题以集合的关系为载体主要考查了函数的单调性于函数的值域的求解,而函数的恒成立的问题的解决常转化为求解函数的最值.

练习册系列答案
相关题目