题目内容
(2011•临汾模拟)偶函数f(x)满足f(x-1)=f(x+1),且在x∈[0,1]时,f(x)=-x+1,则关于x 的方程f(x)=lg(x+1),在x∈[0,9]上解的个数是( )
分析:首先有已知条件推导函数f(x)的性质,再利用函数与方程思想把问题转化,数形结合,即可得解
解答:解:设y1=f(x),y2=lg(x+1)
方程f(x)=lg(x+1)在x∈[0,9]上解的个数,即为函数y1=f(x),y2=lg(x+1)的图象在x∈[0,9]上交点的个数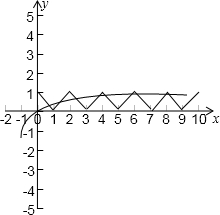
∵f(x-1)=f(x+1)
∴f(x)=f(x+2)
∴原函数的周期T=2
又∵x∈[0,1]时,f(x)=-x+1
由以上条件,可画出y1=f(x),y2=lg(x+1)在x∈[0,9]的图象:
又因为当x=9时,y1≤1,y2=1
∴结合图象可知,在[0,9]上y1=f(x),y2=lg(x+1)的图象共有9个交点
∴在[0,9]上,原方程有9个根
故选C
方程f(x)=lg(x+1)在x∈[0,9]上解的个数,即为函数y1=f(x),y2=lg(x+1)的图象在x∈[0,9]上交点的个数

∵f(x-1)=f(x+1)
∴f(x)=f(x+2)
∴原函数的周期T=2
又∵x∈[0,1]时,f(x)=-x+1
由以上条件,可画出y1=f(x),y2=lg(x+1)在x∈[0,9]的图象:
又因为当x=9时,y1≤1,y2=1
∴结合图象可知,在[0,9]上y1=f(x),y2=lg(x+1)的图象共有9个交点
∴在[0,9]上,原方程有9个根
故选C
点评:本题主要考查了函数的性质,同时考查了转化的思想和函数与方程思想,数形结合思想,属较难题

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目