题目内容
设椭圆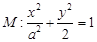
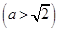 的右焦点为
的右焦点为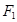 ,直线
,直线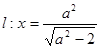 与
与 轴交于点
轴交于点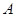 ,若
,若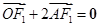 (其中
(其中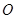 为坐标原点).
为坐标原点).
(1)求椭圆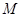 的方程;
的方程;
(2)设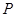 是椭圆
是椭圆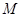 上的任意一点,
上的任意一点,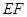 为圆
为圆 的任意一条直径(
的任意一条直径(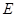 、
、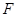 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.
(1)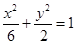 (2)11
(2)11
解析试题分析:
(1)根据题意求出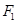 的坐标
的坐标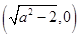 与A点的坐标,带入式子
与A点的坐标,带入式子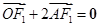 ,即可求出a的值,进而得到椭圆M的方程.
,即可求出a的值,进而得到椭圆M的方程.
(2)设圆 的圆心为
的圆心为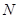 ,则可以转化所求内积,
,则可以转化所求内积,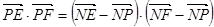
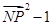 ,故求求
,故求求 的最大值转化为求
的最大值转化为求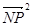 的最大值.N点为定点且坐标已知,故设出P点的坐标且满足椭圆方程,带入坐标公式利用二次函数求最值的方法即可求出NP的最值,此外还可以利用参数方程来求解NP的最值.
的最大值.N点为定点且坐标已知,故设出P点的坐标且满足椭圆方程,带入坐标公式利用二次函数求最值的方法即可求出NP的最值,此外还可以利用参数方程来求解NP的最值.
试题解析:
(1)由题设知,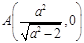 ,
,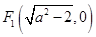 , 1分
, 1分
由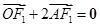 ,得
,得 . 2分
. 2分
解得 . 3分
. 3分
所以椭圆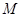 的方程为
的方程为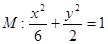 . 4分
. 4分
(2)方法1:设圆 的圆心为
的圆心为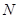 ,
,
则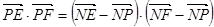 5分
5分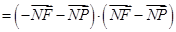 6分
6分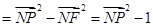 . 7分
. 7分
从而求 的最大值转化为求
的最大值转化为求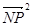 的最大值. 8分
的最大值. 8分
因为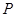 是椭圆
是椭圆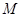 上的任意一点,设
上的任意一点,设 , 9分
, 9分
所以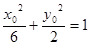 ,即
,即 . 10分
. 10分
因为点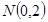 ,所以
,所以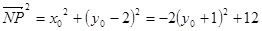 . 11分
. 11分
因为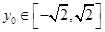 ,所以当
,所以当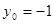 时,
时,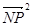 取得最大值12. 13分
取得最大值12. 13分
所以 的最大值为11. 14分
的最大值为11. 14分
方法2:设点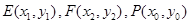 ,
,
因为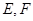 的中点坐标为
的中点坐标为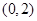 ,所以
,所以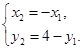 5分
5分
所以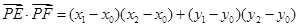 6分
6分

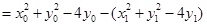 . 8分
. 8分
因为点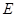 在圆
在圆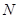 上,所以
上,所以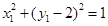 ,即
,即 . 9分
. 9分
因为点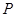 在椭圆
在椭圆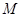 上,所以
上,所以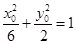 ,即
,即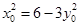 . 10分
. 10分
所以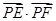
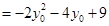
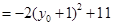 . 12分
. 12分
因为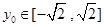 ,所以当
,所以当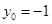 时,
时,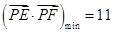 . 14分
. 14分
方法3:①若直线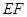 的斜率存在,设
的斜率存在,设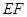 的方程为
的方程为 , 5分
, 5分
由

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
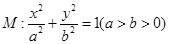 的离心率为
的离心率为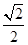 ,且过点
,且过点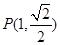 直线
直线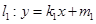 与椭圆M交于A、C两点,直线
与椭圆M交于A、C两点,直线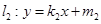 与椭圆M交于B、D两点,四边形ABCD是平行四边形
与椭圆M交于B、D两点,四边形ABCD是平行四边形
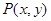 到定点
到定点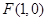 与到定直线,
与到定直线,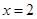 的距离之比为
的距离之比为 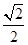 .
.  的轨迹方程;
的轨迹方程;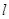 (与x轴不重合)与(1)中轨迹交于两点
(与x轴不重合)与(1)中轨迹交于两点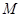 、
、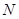 .探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.
.探究是否存在一定点E(t,0),使得x轴上的任意一点(异于点E、F)到直线EM、EN的距离相等?若存在,求出t的值;若不存在,说明理由.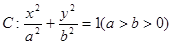 的离心率为
的离心率为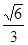 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为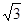 .
.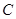 的方程;
的方程;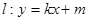 与椭圆
与椭圆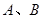 两点,坐标原点
两点,坐标原点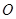 到直线
到直线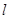 的距离为
的距离为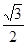 ,求
,求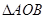 面积的最大值.
面积的最大值.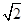 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆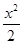 +y2=1有两个不同的交点P和Q.
+y2=1有两个不同的交点P和Q.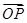 +
+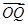 与
与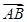 共线?如果存在,求k的值;如果不存在,请说明理由.
共线?如果存在,求k的值;如果不存在,请说明理由. ,且过点M
,且过点M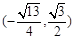 。
。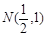 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
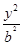 =1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
=1(0<b<1)的左、右焦点,过F1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.