题目内容
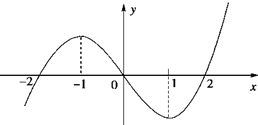
 已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)<0的解集
已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)<0的解集(1,3)
(1,3)
.分析:由f(x)的图象可知:当x<-1或x>1时,函数f(x)单调递增,f′(x)>0;当-1<x<1时,函数f(x)单调递减,f′(x)<0.
不等式(x2-2x-3)f′(x)<0可化为
或
解出即可.
不等式(x2-2x-3)f′(x)<0可化为
|
|
解答:解:由f(x)的图象可知:当x<-1或x>1时,函数f(x)单调递增,∴f′(x)>0;当-1<x<1时,函数f(x)单调递减,f′(x)<0.
不等式(x2-2x-3)f′(x)<0可化为
或
化为
或
,
解得∅或1<x<3.
∴不等式(x2-2x-3)f′(x)<0的解集是(1,3).
故答案为(1,3).
不等式(x2-2x-3)f′(x)<0可化为
|
|
化为
|
|
解得∅或1<x<3.
∴不等式(x2-2x-3)f′(x)<0的解集是(1,3).
故答案为(1,3).
点评:熟练掌握函数的单调性与当时的关系、不等式的解法、数形结合的思想方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
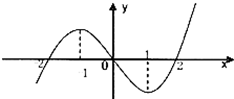
 9、已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( )
9、已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( ) 已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( )
已知R上可导函数f(x)的图象如图所示,则不等式(x2-2x-3)f′(x)>0的解集为( )