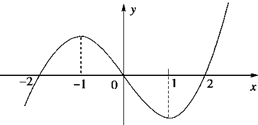
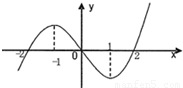
题目内容
9、已知R上可导函数f（x）的图象如图所示，则不等式（x2-2x-3）f′（x）＞0的解集为（ ）分析：根据题意结合图象求出f′（x）＞0的解集与f′（x）＜0的解集，因此对原不等式进行化简与转化，进而得到原不等式的答案．
解答：解：由图象可得：当f′（x）＞0时，函数f（x）是增函数，所以f′（x）＞0的解集为（-∞，-1），（1，+∞），
当f′（x）＜0时，函数f（x）是减函数，所以f′（x）＜0的解集为（-1，1）．
所以不等式f′（x）＜0即与不等式（x-1）（x+1）＜0的解集相等．
由题意可得：不等式（x2-2x-3）f′（x）＞0等价于不等式（x-3）（x+1）（x+1）（x-1）＞0，
所以原不等式的解集为（-∞，-1）∪（-1，1）∪（3，+∞），
故选D．
当f′（x）＜0时，函数f（x）是减函数，所以f′（x）＜0的解集为（-1，1）．
所以不等式f′（x）＜0即与不等式（x-1）（x+1）＜0的解集相等．
由题意可得：不等式（x2-2x-3）f′（x）＞0等价于不等式（x-3）（x+1）（x+1）（x-1）＞0，
所以原不等式的解集为（-∞，-1）∪（-1，1）∪（3，+∞），
故选D．
点评：解决此类问题的关键是熟悉函数的单调性与导数的关系，以及掌握读图与识图的技巧再结合不等式的解法即可得到答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
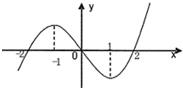
已知R上可导函数f（x）的图象如图所示，则不等式（x2-2x-3）f′（x）＜0的解集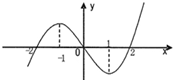
已知R上可导函数f（x）的图象如图所示，则不等式（x2-2x-3）f′（x）＞0的解集为（ ）
