题目内容
函数y=f（x）与y=g（x）有相同的定义域，且都不是常数函数，对定义域中任意x，有f（x）+f（-x）=0，g（x）g（-x）=1，且x≠0，g（x）≠1，则F（x）=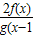
+f（x）（ ）A．是奇函数但不是偶函数
B．是偶函数但不是奇函数
C．既是奇函数又是偶函数
D．既不是奇函数也不是偶函数
【答案】分析：由已知中f（x）+f（-x）=0，g（x）g（-x）=1，且x≠0，g（x）≠1，则F（x）=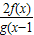
+f（x），我们求出F（-x）的解析式，然后根据函数奇偶性的定义即可得到答案．
解答：解：由条件f（-x）=-f（x），g（x）g（-x）=1，F（x）=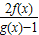
+f（x）得：
F（-x）=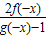
+f（-x）
=
=
=
=
=
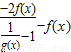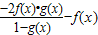
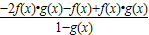
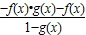
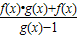=F（x），
故F（x）=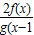
+f（x）为偶函数，
故选B．
点评：本题考查的知识点是抽象函数及其应用，其中根据已知条件求出函数F（-x）的解析式，是解答本题的关键．
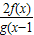+f（x），我们求出F（-x）的解析式，然后根据函数奇偶性的定义即可得到答案．解答：解：由条件f（-x）=-f（x），g（x）g（-x）=1，F（x）=
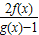+f（x）得：F（-x）=
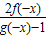+f（-x）=
==
=
=
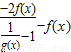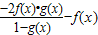
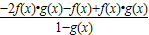
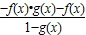
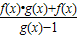=F（x），故F（x）=
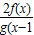+f（x）为偶函数，故选B．
点评：本题考查的知识点是抽象函数及其应用，其中根据已知条件求出函数F（-x）的解析式，是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目