题目内容
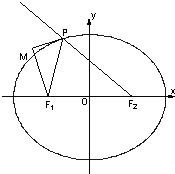
已知如图,椭圆方程为 (4>b>0).P为椭圆上的动点,
(4>b>0).P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;
(2)已知O(0,0)、E(2,1),试探究是否存在这样的点Q:Q是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积S△OEQ=2?若存在,求出点Q的坐标,若不存在,说明理由.

【答案】分析:(1)延长F1M与F2P的延长线相交于点N,连接OM,利用条件求出M是线段NF1的中点,转化出|OM|=4即可求出M点的轨迹T的方程;
(2)可以先观察出轨迹T上有两个点A(-4,0),B(4,0)满足S△OEA=S△OEB=2,再利用同底等高的两个三角形的面积相等,,,知道符合条件的点均在过A、B作直线OE的两条平行线l1、l2上,再利用点Q是轨迹T内部的整点即可求出点Q的坐标.
解答: 解:(1)当点P不在x轴上时,延长F1M与F2P的延长线相交于点N,连接OM,
解:(1)当点P不在x轴上时,延长F1M与F2P的延长线相交于点N,连接OM,
∵∠NPM=∠MPF1,∠NMP=∠PMF1
∴△PNM≌△PF1M
∴M是线段NF1的中点,|PN|=|PF1||(2分)
∴|OM|= |F2N|=
|F2N|= (|F2P|+|PN|)=
(|F2P|+|PN|)= (|F2P|+|PF1|)
(|F2P|+|PF1|)
∵点P在椭圆上
∴|PF2|+|PF1|=8∴|OM|=4,(4分)
当点P在x轴上时,M与P重合
∴M点的轨迹T的方程为:x2+y2=42.(6分)
 (2)连接OE,易知轨迹T上有两个点
(2)连接OE,易知轨迹T上有两个点
A(-4,0),B(4,0)满足S△OEA=S△OEB=2,
分别过A、B作直线OE的两条平行线l1、l2.
∵同底等高的两个三角形的面积相等
∴符合条件的点均在直线l1、l2上.(7分)
∵
∴直线l1、l2的方程分别为: 、
、 (8分)
(8分)
设点Q(x,y)(x,y∈Z)∵Q在轨迹T内,
∴x2+y2<16(9分)
分别解 与
与
得 与
与 (11分)
(11分)
∵x,y∈Z
∴x为偶数,在 上x=-2,,0,2对应的y=1,2,3
上x=-2,,0,2对应的y=1,2,3
在 上x=-2,0,2,对应的y=-3,-2,-1(13分)
上x=-2,0,2,对应的y=-3,-2,-1(13分)
∴满足条件的点Q存在,共有6个,
它们的坐标分别为:(-2,1),(0,2),(2,3),(-2,-3),(0,-2),(2,-1).(14分)
点评:本题涉及到轨迹方程的求法.在求动点的轨迹方程时,一般多是利用题中条件得出关于动点坐标的等式,整理可得动点的轨迹方程.
(2)可以先观察出轨迹T上有两个点A(-4,0),B(4,0)满足S△OEA=S△OEB=2,再利用同底等高的两个三角形的面积相等,,,知道符合条件的点均在过A、B作直线OE的两条平行线l1、l2上,再利用点Q是轨迹T内部的整点即可求出点Q的坐标.
解答:
 解:(1)当点P不在x轴上时,延长F1M与F2P的延长线相交于点N,连接OM,
解:(1)当点P不在x轴上时,延长F1M与F2P的延长线相交于点N,连接OM,∵∠NPM=∠MPF1,∠NMP=∠PMF1
∴△PNM≌△PF1M
∴M是线段NF1的中点,|PN|=|PF1||(2分)
∴|OM|=
 |F2N|=
|F2N|= (|F2P|+|PN|)=
(|F2P|+|PN|)= (|F2P|+|PF1|)
(|F2P|+|PF1|)∵点P在椭圆上
∴|PF2|+|PF1|=8∴|OM|=4,(4分)
当点P在x轴上时,M与P重合
∴M点的轨迹T的方程为:x2+y2=42.(6分)
 (2)连接OE,易知轨迹T上有两个点
(2)连接OE,易知轨迹T上有两个点A(-4,0),B(4,0)满足S△OEA=S△OEB=2,
分别过A、B作直线OE的两条平行线l1、l2.
∵同底等高的两个三角形的面积相等
∴符合条件的点均在直线l1、l2上.(7分)
∵

∴直线l1、l2的方程分别为:
 、
、 (8分)
(8分)设点Q(x,y)(x,y∈Z)∵Q在轨迹T内,
∴x2+y2<16(9分)
分别解
 与
与
得
 与
与 (11分)
(11分)∵x,y∈Z
∴x为偶数,在
 上x=-2,,0,2对应的y=1,2,3
上x=-2,,0,2对应的y=1,2,3在
 上x=-2,0,2,对应的y=-3,-2,-1(13分)
上x=-2,0,2,对应的y=-3,-2,-1(13分)∴满足条件的点Q存在,共有6个,
它们的坐标分别为:(-2,1),(0,2),(2,3),(-2,-3),(0,-2),(2,-1).(14分)
点评:本题涉及到轨迹方程的求法.在求动点的轨迹方程时,一般多是利用题中条件得出关于动点坐标的等式,整理可得动点的轨迹方程.

练习册系列答案
相关题目
 已知如图,椭圆方程为
已知如图,椭圆方程为 (本题满分14分)已知如图,椭圆方程为
(本题满分14分)已知如图,椭圆方程为 (4>b>0).P为椭圆上的动点,
(4>b>0).P为椭圆上的动点,