题目内容
函数 的图象可以由函数g(x)=4sinxcosx的图象( )而得到.
的图象可以由函数g(x)=4sinxcosx的图象( )而得到.A.向左平移
 个单位
个单位B.向右平移
 个单位
个单位C.向左平移
 个单位
个单位D.向右平移
 个单位
个单位
【答案】分析:利用两角和差的正弦公式化简f(x)的解析式为 2sin2(x- ),利用二倍角公式化简函数g(x)的解析式为 2sin2x,再根据函数y=Asin(ωx+∅)的图象变换规律,得出结论.
),利用二倍角公式化简函数g(x)的解析式为 2sin2x,再根据函数y=Asin(ωx+∅)的图象变换规律,得出结论.
解答:解:∵函数 =2(
=2( -
- )=2sin(2x-
)=2sin(2x- )=2sin2(x-
)=2sin2(x- ),
),
函数g(x)=4sinxcosx=2sin2x,
故把g(x)=2sin2x的图象向右平移 个单位,即可得到f(x)=2sin2(x-
个单位,即可得到f(x)=2sin2(x- )的图象,
)的图象,
故选D.
点评:本题主要考查两角和差的正弦公式的应用,函数y=Asin(ωx+∅)的图象变换规律,属于中档题.
 ),利用二倍角公式化简函数g(x)的解析式为 2sin2x,再根据函数y=Asin(ωx+∅)的图象变换规律,得出结论.
),利用二倍角公式化简函数g(x)的解析式为 2sin2x,再根据函数y=Asin(ωx+∅)的图象变换规律,得出结论.解答:解:∵函数
 =2(
=2( -
- )=2sin(2x-
)=2sin(2x- )=2sin2(x-
)=2sin2(x- ),
),函数g(x)=4sinxcosx=2sin2x,
故把g(x)=2sin2x的图象向右平移
 个单位,即可得到f(x)=2sin2(x-
个单位,即可得到f(x)=2sin2(x- )的图象,
)的图象,故选D.
点评:本题主要考查两角和差的正弦公式的应用,函数y=Asin(ωx+∅)的图象变换规律,属于中档题.

练习册系列答案
相关题目
 ,则
,则 ,均有
,均有 ;
; 切线斜率的最大值是2;
切线斜率的最大值是2; 则
则
 的图象可以由函数
的图象可以由函数 的图象仅通过平移变换得到;
的图象仅通过平移变换得到;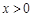 且
且 时,有
时,有 ②
② 中,
中, 是
是 成立的充要条件;③函数
成立的充要条件;③函数 的图象可以由函数
的图象可以由函数
 (其中
(其中 且
且 的图象通过平移得到;④已知
的图象通过平移得到;④已知 是等差数列
是等差数列 的前
的前 项和,若
项和,若 则
则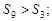 ⑤函数
⑤函数 与函数
与函数 的图象关于直线
的图象关于直线 对称,,其中正确命题的序号为 .
对称,,其中正确命题的序号为 . 的图象可以由函数
的图象可以由函数 的图象
的图象 个单位得到(B)向右平移-
个单位得到(B)向右平移- 个单位得到
个单位得到 个单位得到(D)向右平移
个单位得到(D)向右平移 个单位得到
个单位得到