题目内容
已知 ,
, ,且
,且 .求:
.求:
(1) 的值;(2)
的值;(2) 的值.
的值.
 ,
, ,且
,且 .求:
.求:(1)
 的值;(2)
的值;(2) 的值.
的值.(1)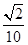 ;(2)
;(2)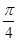 。
。
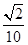 ;(2)
;(2)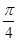 。
。试题分析:(1)因为
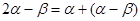 ,故求出
,故求出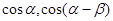 ,然后用用两角和的余弦可求出
,然后用用两角和的余弦可求出 的值;(2)因为
的值;(2)因为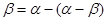 ,
,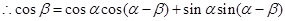 ,把(1)中的结论代入可得
,把(1)中的结论代入可得 的余弦值。
的余弦值。 试题解析:(1)因为
 ,所以
,所以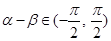 , (1分)
, (1分)∵
 ,∴
,∴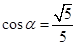 (2分)
(2分)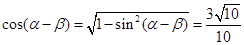 , (3分)
, (3分)∴
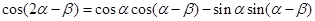 (5分)
(5分)=
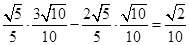 (7分)
(7分)(2)
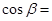
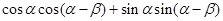 (9分)
(9分)=
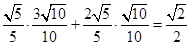 ,又∵
,又∵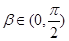 ,∴
,∴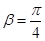 (12分)
(12分)
练习册系列答案
相关题目
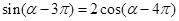 ;求
;求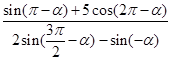 的值.
的值.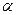 为第二象限角,那么
为第二象限角,那么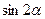 ,
,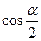 ,
,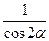 ,
,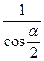 中,其值必为正的有
中,其值必为正的有 个
个 个
个 个
个 个
个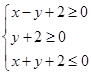 内一点
内一点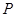 作圆
作圆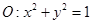 的两条切线,切点分别为
的两条切线,切点分别为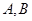 ,记
,记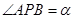 ,则当
,则当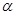 最小时
最小时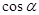 的值为( )
的值为( )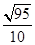
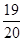
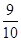
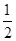
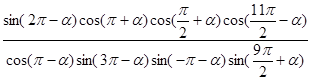 .
. ,则
,则 ______________.
______________.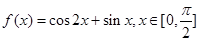 的值域为
的值域为 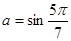 ,
,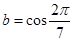 ,
,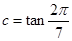 ,则
,则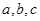 的大小关系为 (按由小至大顺序排列)
的大小关系为 (按由小至大顺序排列)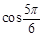 的值等于 .
的值等于 .