题目内容
（06年辽宁卷理）（12分）
已知
,其中
,
设
,
.
(I) 写出
;
(II) 证明:对任意的
,恒有
.
解析: (I)由已知推得
,从而有
(II) 证法1:当
时,
当x>0时, 
,所以
在[0,1]上为增函数
因函数为偶函数所以在[-1,0]上为减函数
所以对任意的
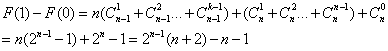
因此结论成立.
证法2: 当时,
当x>0时, ,所以在[0,1]上为增函数
因函数为偶函数所以在[-1,0]上为减函数
所以对任意的
又因
所以
因此结论成立.
证法3: 当时,
当x>0时, ,所以在[0,1]上为增函数
因函数为偶函数所以在[-1,0]上为减函数
所以对任意的
由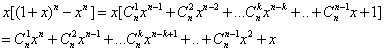
对上式两边求导得
因此结论成立.
练习册系列答案
名校课堂系列答案
相关题目
,则
的值域是
(B) 
(C) 
(D) 
、
、
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,对乙项目每投资十万元, 
、
分别表示对甲、乙两项目各投资十万元一年后的利润.
、
;
时,求
的取值范围.
,其中a , b , c是以d为公差的等差数列，，且a＞0,d＞0.设
［1-
］上，
，在
，将点
A， B， C
，求a ,d的值