题目内容
在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值如下表:x(s) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
y(μm) | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
(1)画出表中数据的散点图;
(2)求y对x的回归直线方程;
(3)试预测腐蚀时间为100 s时腐蚀深度是多少.
解析:(1)散点图如下图所示:

(2)根据公式求腐蚀深度y对腐蚀时间x的回归直线方程的步骤如下:
先把数据列成表:
i | xi | yi |
|
| xiyi |
1 | 5 | 6 | 25 | 36 | 30 |
2 | 10 | 10 | 100 | 100 | 100 |
3 | 15 | 10 | 225 | 100 | 150 |
4 | 20 | 13 | 400 | 169 | 260 |
5 | 30 | 16 | 900 | 256 | 480 |
6 | 40 | 17 | 1 600 | 289 | 680 |
7 | 50 | 19 | 2 500 | 361 | 950 |
8 | 60 | 23 | 3 600 | 529 | 1 380 |
9 | 70 | 25 | 4 900 | 625 | 1 750 |
10 | 90 | 29 | 8 100 | 841 | 2 610 |
11 | 120 | 46 | 14 400 | 2 116 | 5 520 |
| 510 | 214 | 36 750 | 5 422 | 13 910 |
计算a,b的值.
由上表分别计算x,y平均数得:
![]() =
=![]() ,
,![]() =
=![]() ,
,
代入公式
b=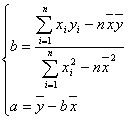 得(注意:不必把
得(注意:不必把![]() ,
,![]() 化为小数,以减小误差),
化为小数,以减小误差),
b=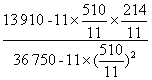 ≈0.304,
≈0.304,
a=![]() -0.304×
-0.304×![]() =5.36.
=5.36.
写出回归直线方程.
腐蚀深度y对腐蚀时间x的回归直线方程为:
![]() =0.304x+5.36,
=0.304x+5.36,
这里的回归系数b=0.304,它的意义是:腐蚀时间x每增加一个单位(s),深度y增加0.304个单位(μm).
(3)根据上面求得的回归直线方程,当腐蚀时间为100 s时,
![]() =0.304×100+5.36=35.76(μm),即腐蚀深度大约是35.76 μm.
=0.304×100+5.36=35.76(μm),即腐蚀深度大约是35.76 μm.

练习册系列答案
相关题目
在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y与腐蚀时间x的一组数据如下表所示:
x(秒) | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 |
y(微米) | 6 | 10 | 11 | 13 | 16 | 17 | 19 | 23 |
(1)画出数据的散点图.
(2)根据散点图,你能得出什么结论?
 在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y与腐蚀时间x的一组数据如表所示:
在某种产品表面进行腐蚀刻线试验,得到腐蚀深度y与腐蚀时间x的一组数据如表所示: