题目内容
1.设奇函数f(x)在(0,+∞)上为增函数,且f(3)=0,则不等式$\frac{f(x)-f(-x)}{2}$>0的解集为( )| A. | (-3,0)∪(3,+∞) | B. | (-3,0)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-∞,-3)∪(0,3) |
分析 根据条件可得到f(-3)=0,f(x)在(-∞,0)上单调递增,从而由不等式$\frac{f(x)-f(-x)}{2}>0$便可得到f(x)>0,讨论x:x>0时,会得到f(x)>f(3);x<0时,会得到f(x)>f(-3),这样根据f(x)的单调性便可得出这两种情况下x的范围,求并集便可得出原不等式的解集.
解答 解:f(x)为奇函数,f(3)=0;
∴f(-3)=0;
f(x)在(0,+∞)上为增函数;
∴f(x)在(-∞,0)上为增函数;
∴$\frac{f(x)-f(-x)}{2}=f(x)>0$;
①若x>0,则f(x)>f(3);
∴x>3;
②若x<0,则f(x)>f(-3);
∴-3<x<0;
∴综上得原不等式的解集为(-3,0)∪(3,+∞).
故选A.
点评 考查奇函数的定义,奇函数在对称区间上的单调性特点,以及增函数的定义,根据单调性解不等式的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知某个几何体的三视图如下,根据图中标出的尺寸,那么可得这个几何体最长的棱长是( )


| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
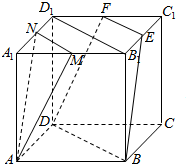 已知在正方体ABCD-A1B1C1D1中,M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点.求证:
已知在正方体ABCD-A1B1C1D1中,M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点.求证: