题目内容
)设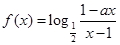 为奇函数,
为奇函数,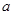 为常数.
为常数.
(1)求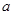 的值;
的值;
(2)判断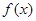 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;
(3)若对于区间 [3,4]上的每一个 的值,不等式
的值,不等式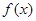 >
>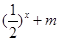 恒成立,求实数
恒成立,求实数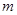 的取值范围.
的取值范围.
【答案】
(1)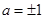 (2)在(1,+∞)上是增函数(3)
(2)在(1,+∞)上是增函数(3)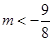
【解析】
试题分析:解:(1)∵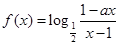 为奇函数,
为奇函数,
∴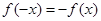 对于
对于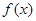 定义域中任意实数恒成立,
定义域中任意实数恒成立,
即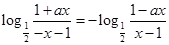 2分
2分
∴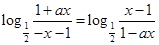 ∴
∴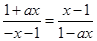 ∴
∴
∴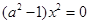 对于
对于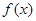 定义域中任意实数恒成立
定义域中任意实数恒成立
∵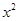 不恒为0,∴
不恒为0,∴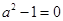 ∴
∴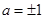 4分
4分
当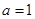 时
时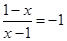 不符题意
不符题意
∴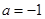 5分
5分
(2)由(1)得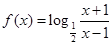
设1<x1<x2,则
f(x1)-f(x2)=log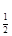
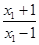 -log
-log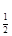
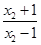 =log
=log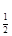
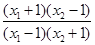
=log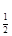
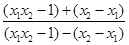 7分
7分
∵ 1<x1<x2,∴ x2-x1>0,
∴ (x1x2-1)+(x2-x1)>(x1x2-1)-(x2-x1)>0
即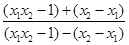 >1. 9分
>1. 9分
∴ f(x1)-f(x2)<0即f(x1)<f(x2),在(1,+∞)上是增函数 10分
(3)由(1),不等式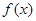 >
>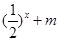 可化为
可化为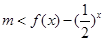 ,即
,即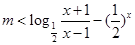
由题意得对于区间[3,4]上的每一个 的值,
的值,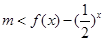 恒成立 2分
恒成立 2分
令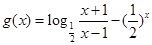 ,则
,则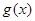 区间[3,4]上为增函数
区间[3,4]上为增函数
∵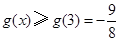 ∴
∴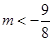 15分
15分
考点:函数性质的综合运用
点评:解决的关键是对于函数奇偶性和单调性的灵活运用,以及利用分离参数的思想求解函数的最值得到范围。属于中档题。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
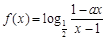 为奇函数,
为奇函数,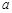 为常数.
为常数.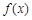 在区间(1,+∞)的单调性,并说明理由;
在区间(1,+∞)的单调性,并说明理由;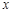 值,不等式
值,不等式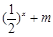 恒成立,求实数
恒成立,求实数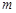 的取值范围.
的取值范围. 为奇函数,
为奇函数,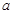 为常数。
为常数。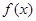 在(1,+∞)内单调递增;
在(1,+∞)内单调递增;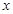 的值,不等式
的值,不等式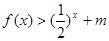 恒成立,求实数
恒成立,求实数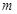 的取值范围。
的取值范围。