题目内容
用0,1,2,…,9十个数字可组成多少个没有重复数字的:(1)五位奇数?
(2)大于30 000的五位偶数?
解析:(1)要得到五位奇数,末位应从1,3,5,7,9五个数字中取,有![]() 种取法.取定末位数字后,首位就有除这个数字和0之外的八种不同取法.首末两位取定后,十个数字还有八个数字可供中间的十位,百位与千位三个数位选取,共有
种取法.取定末位数字后,首位就有除这个数字和0之外的八种不同取法.首末两位取定后,十个数字还有八个数字可供中间的十位,百位与千位三个数位选取,共有![]() 种不同的安排方法.因此由分步计数原理共有5×8×
种不同的安排方法.因此由分步计数原理共有5×8×![]() =13 440个没有重复数字的五位奇数.
=13 440个没有重复数字的五位奇数.
(2)要得偶数,末位应从0,2,4,6,8中选取,而要得比30 000大的五位偶数,可分两类:
①末位数字从0,2中选取,则首位可取3、4、5、6、7、8、9中任一个,共7种选取方法,其余三个数位就有除首末两个数位上的数字之外的八个数字可以选取,共![]() 种取法.所以共有2×7×
种取法.所以共有2×7×![]() 种不同情况.
种不同情况.
②末位数字从4、6、8中选取,则首位应从3、4、5、6、7、8、9中除去末位数字的六个数字中选取,其余三个数位仍有![]() 种选法,所以共有3×6×
种选法,所以共有3×6×![]() 种不同情况.
种不同情况.
由分类计数原理,共有2×7×![]() +3×6×
+3×6×![]() =10 752个比30 000大的无重复数字的五位偶数.
=10 752个比30 000大的无重复数字的五位偶数.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
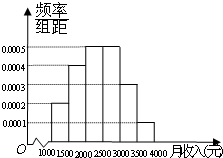 (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图). (2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).
(2012•梅州二模)一个社会调查机构就某社区居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).