题目内容
下列几个命题①方程x2+(a-3)x+a=0的有一个正实根,一个负实根,则a<0.
②函数
 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-3,1].
④设函数y=f(x)定义域为R且满足f(x-1)=f(1-x),则函数y=f(x)的图象关于y轴对称.
⑤曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,则m的值不可能是1.
其中正确的有 .
【答案】分析:用根的分布来解,令f(x)=x2+2(m-1)x+2m+6,一个比0大,一个比0小,只要f(0)<0即可.
函数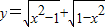 =0,既是偶函数,又是奇函数;函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2];设函数y=f(x)定义域为R且满足f(1-x)=f(1-x),则它的图象关于x=0对称;一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,画出函数的图象,根据图象进行判断:m的值不可能是1.
=0,既是偶函数,又是奇函数;函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2];设函数y=f(x)定义域为R且满足f(1-x)=f(1-x),则它的图象关于x=0对称;一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,画出函数的图象,根据图象进行判断:m的值不可能是1.
解答:解:①方程x2+(a-3)x+a=0有一个正实根,一个负实根,则a<0;正确;
②函数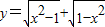 =0,函数的定义域为{-1,1},∴y=0既是奇函数又是偶函数既是偶函数,故②不正确;
=0,函数的定义域为{-1,1},∴y=0既是奇函数又是偶函数既是偶函数,故②不正确;
 ③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2].故③不正确;
③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2].故③不正确;
④设函数y=f(x)定义域为R且满足f(x-1)=f(1-x),则有:f(-x)=f(x),它的图象关于y轴对称.故④正确;
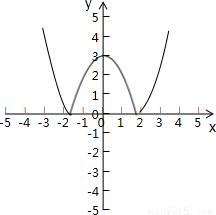
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,根据函数y=|3-x2|的图象可知:m的值不可能是1.故⑤正确.
故答案为:①④⑤.
点评:考查了函数思想,转化思想,属中档题,是个基础题.还考查函数图象的对称变化和一元二次方程根的问题,以及函数奇偶性的判定方法等基础知识,考查学生灵活应用知识分析解决问题的能力,数形结合法是解答本类题的重要方法.
函数
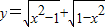 =0,既是偶函数,又是奇函数;函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2];设函数y=f(x)定义域为R且满足f(1-x)=f(1-x),则它的图象关于x=0对称;一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,画出函数的图象,根据图象进行判断:m的值不可能是1.
=0,既是偶函数,又是奇函数;函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2];设函数y=f(x)定义域为R且满足f(1-x)=f(1-x),则它的图象关于x=0对称;一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,画出函数的图象,根据图象进行判断:m的值不可能是1.解答:解:①方程x2+(a-3)x+a=0有一个正实根,一个负实根,则a<0;正确;
②函数
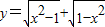 =0,函数的定义域为{-1,1},∴y=0既是奇函数又是偶函数既是偶函数,故②不正确;
=0,函数的定义域为{-1,1},∴y=0既是奇函数又是偶函数既是偶函数,故②不正确; ③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2].故③不正确;
③函数f(x)的值域是[-2,2],则函数f(x+1)的值域为[-2,2].故③不正确;④设函数y=f(x)定义域为R且满足f(x-1)=f(1-x),则有:f(-x)=f(x),它的图象关于y轴对称.故④正确;
⑤一条曲线y=|3-x2|和直线y=a(a∈R)的公共点个数是m,根据函数y=|3-x2|的图象可知:m的值不可能是1.故⑤正确.
故答案为:①④⑤.
点评:考查了函数思想,转化思想,属中档题,是个基础题.还考查函数图象的对称变化和一元二次方程根的问题,以及函数奇偶性的判定方法等基础知识,考查学生灵活应用知识分析解决问题的能力,数形结合法是解答本类题的重要方法.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
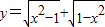 是偶函数,但不是奇函数.
是偶函数,但不是奇函数.