题目内容
已知圆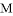 :
: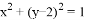 ,
,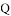 是
是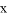 轴上的动点,
轴上的动点, 分别切圆
分别切圆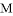 于
于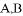 两点.
两点.
(1)若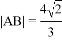 ,求
,求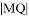 及直线
及直线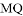 的方程;
的方程;
(2)求证:直线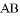 恒过定点.
恒过定点.
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
题目内容
已知圆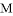 :
: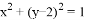 ,
,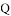 是
是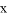 轴上的动点,
轴上的动点, 分别切圆
分别切圆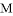 于
于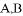 两点.
两点.
(1)若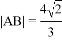 ,求
,求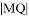 及直线
及直线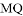 的方程;
的方程;
(2)求证:直线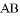 恒过定点.
恒过定点.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案