题目内容
下列命题中正确的有( )①若向量a与b满足a•b<0,则a与b所成角为钝角;
②若向量a与b不共线,m=λ1•a+λ2•b,n=μ1•a+μ2•b,(λ1,λ2μ1,μ2∈R),则m∥n的充要条件是λ1•μ2-λ2•μ1=0;
③若
 ,且
,且 ,则△ABC是等边三角形;
,则△ABC是等边三角形;④若a与b非零向量,a⊥b,则|a+b|=|a-b|.
A.②③④
B.①②③
C.①④
D.②
【答案】分析:通过a与b所成角为180°时a•b<0,但180°不是钝角,排除BC
若a与b非零向量且a⊥b时,|a+b|=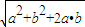 =
=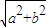
|a-b|=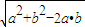 =
=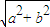 ,∴|a+b|=|a-b|.排除D.
,∴|a+b|=|a-b|.排除D.
解答:解:①a与b所成角为180°时a•b<0,但180°不是钝角,故①不对,排除BC
若a与b非零向量且a⊥b时,|a+b|=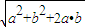 =
=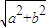
|a-b|=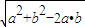 =
=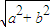 ,∴|a+b|=|a-b|.成立,排除D.
,∴|a+b|=|a-b|.成立,排除D.
故选A.
点评:本题主要考查向量的数量积的性质和利用数量积的运算求模的问题.属基础题.
若a与b非零向量且a⊥b时,|a+b|=
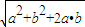 =
=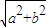
|a-b|=
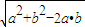 =
=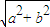 ,∴|a+b|=|a-b|.排除D.
,∴|a+b|=|a-b|.排除D.解答:解:①a与b所成角为180°时a•b<0,但180°不是钝角,故①不对,排除BC
若a与b非零向量且a⊥b时,|a+b|=
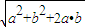 =
=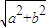
|a-b|=
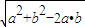 =
=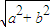 ,∴|a+b|=|a-b|.成立,排除D.
,∴|a+b|=|a-b|.成立,排除D.故选A.
点评:本题主要考查向量的数量积的性质和利用数量积的运算求模的问题.属基础题.

练习册系列答案
相关题目