题目内容
已知正实数x1,x2及函数f(x),满足4x=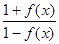 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值
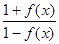 ,且f(x1)+f(x2)=1,则f(x1+x2)的最小值
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值| A.4 | B.2 | C.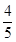 | D.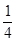 |
C
解:由已知须先求出f(x)的解析式f(x) =(4x-1)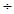 (4x+1 )
(4x+1 )
,然后代入x1,x2及f(x1)+f(x2)=1可得含有入x1,x2的式子
4x1+x2-3=4x1+4x2,再利用均值不等式求出4x1+x2的范围,即可解答f(x1+x2)的最小值为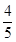
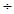 (4x+1 )
(4x+1 ),然后代入x1,x2及f(x1)+f(x2)=1可得含有入x1,x2的式子
4x1+x2-3=4x1+4x2,再利用均值不等式求出4x1+x2的范围,即可解答f(x1+x2)的最小值为
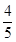

练习册系列答案
相关题目
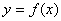 是定义在
是定义在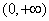 上的减函数,并且满足
上的减函数,并且满足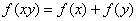 ,
,
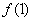 ,
,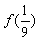 ,
,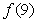 的值,(2)如果
的值,(2)如果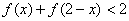 ,求x的取值范围。
,求x的取值范围。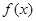 是定义在R上的奇函数,且
是定义在R上的奇函数,且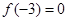 。当
。当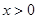 时,有
时,有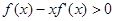 成立,则不等式
成立,则不等式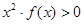 的解集是
的解集是

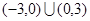
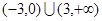
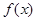 =
=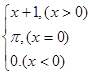 求
求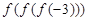 的值。
的值。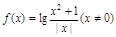 ,有下列命题:
,有下列命题: 轴对称; ②当
轴对称; ②当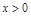 时,
时,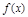 是增函数;当
是增函数;当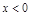 时,
时,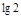 ; ④当
; ④当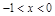 和
和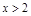 时,
时,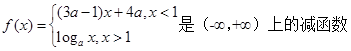 ,那么
,那么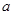 的取值范围( )
的取值范围( ) 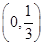 C.
C.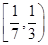 D.
D.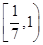
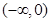 上是增函数的是( )
上是增函数的是( )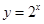
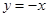
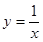
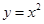
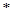 ”表示一种两个正实数之间的运算,即
”表示一种两个正实数之间的运算,即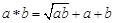 ,则函数
,则函数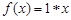 的值域是 .
的值域是 .