题目内容
设P为曲线C:y=ex上的点,若曲线C在点P处的切线不经过第四象限,则该切线的斜率的取值范围是
(0,e]
(0,e]
.分析:欲求曲线C在点P处的切线不经过第四象限,该切线的斜率的取值范围,先设切点的坐标为( ${x_0},{e^{x_0}})$,,再求出在点切点( ${x_0},{e^{x_0}})$处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=x0处的导函数值,再结合导数的几何意义即可求出切线的斜率.最后利用切线过原点即可解决问题.
解答:解:y′=ex
设切点的坐标为(x0,ex0),切线的斜率为k,
则k=ex0,故切线方程为y-ex0=ex0(x-x0)
又切线过原点,∴-ex0=ex0(-x0),
∴x0=1,y0=e,k=e.
若曲线C在点P处的切线不经过第四象限,则该切线的斜率的取值范围是(0,e].
故答案为:(0,e].
设切点的坐标为(x0,ex0),切线的斜率为k,
则k=ex0,故切线方程为y-ex0=ex0(x-x0)
又切线过原点,∴-ex0=ex0(-x0),
∴x0=1,y0=e,k=e.
若曲线C在点P处的切线不经过第四象限,则该切线的斜率的取值范围是(0,e].
故答案为:(0,e].
点评:本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 ,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于
,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于 .设点M的轨迹为曲线C,经过点
.设点M的轨迹为曲线C,经过点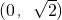 且斜率为k的直线l与曲线C有两个不同的交点P和Q.
且斜率为k的直线l与曲线C有两个不同的交点P和Q.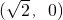 ,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量
,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量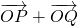 与
与 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.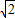 ,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于
,0)关于原点O对称,M是动点,且直线EM与FM的斜率之积等于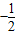 .设点M的轨迹为曲线C,经过点
.设点M的轨迹为曲线C,经过点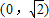 且斜率为k的直线l与曲线C有两个不同的交点P和Q.
且斜率为k的直线l与曲线C有两个不同的交点P和Q.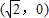 ,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量
,曲线C与y轴正半轴的交点为B,是否存在常数k,使得向量 与
与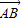 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.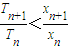 (n∈N+).
(n∈N+).
 (n∈N+).
(n∈N+).