题目内容
已知方程|x|-ax-1=0仅有一个负根,则a的取值范围是( )A.a<1
B.a≤1
C.a>1
D.a≥1
【答案】分析:由方程|x|-ax-1=0仅有一个负根,知函数y=|x|-1与函数y=ax的图象只在左半平面有一个交点,由此能求出a的取值范围.
解答: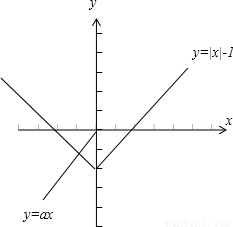 解:∵方程|x|-ax-1=0仅有一个负根,
解:∵方程|x|-ax-1=0仅有一个负根,
∴函数y=|x|-1=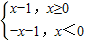 与函数y=ax的图象只在左半平面有一个交点.
与函数y=ax的图象只在左半平面有一个交点.
在同一平面内分别作出y=|x|-1= 与函数y=ax的图象:
与函数y=ax的图象:
观察图象知:a≥1.
故选D.
点评:本题考查函数的零点的性质的应用,解题时要认真审题,注意数形结合思想的合理运用.
解答:
 解:∵方程|x|-ax-1=0仅有一个负根,
解:∵方程|x|-ax-1=0仅有一个负根,∴函数y=|x|-1=
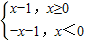 与函数y=ax的图象只在左半平面有一个交点.
与函数y=ax的图象只在左半平面有一个交点.在同一平面内分别作出y=|x|-1=
 与函数y=ax的图象:
与函数y=ax的图象:观察图象知:a≥1.
故选D.
点评:本题考查函数的零点的性质的应用,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目