题目内容
为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民户电价为每千瓦时0.53元.若总用电量为S千瓦时,设高峰时段用电量为x千瓦时.
(1)写出实行峰谷电价的电费y1=g1(x)及现行电价的电费y2=g2(S)的函数解析式及电费总差额f(x)=y2-y1的解析式;
(2)对于用电量按时均等的电器(在全天任何相同长的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?说明你的理由..
解:(1)若总用电量为S千瓦时,设高锋时段用电量为x千瓦时,则低谷时段用电量为(S-x)千瓦时;
实行峰谷电价的电费为y1=0.56x+(S-x)×0.28=0.28S+0.28x;
现行电价的电费为y2=0.53S;
电费总差额f(x)=y2-y1=0.25S-0.28x,(0≤x≤S)
(2)可以省钱,因为f(x)>0,即0.25S-0.28x>0,∴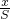 <
<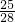 .
.
对于用电量按时均等的电器,高峰用电时段的时间与总时间的比为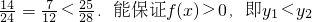 .
.
所以用电量按时均等的电器采用峰谷电价的计费方法后能省钱.
分析:(1)总用电量为S千瓦时,高锋时段用电量为x千瓦时,则低谷时段用电量为(S-x)千瓦时;实行峰谷电价的电费y1=0.56x+(S-x)×0.28;现行电价的电费y2=0.53S;作差比较y2-y1即可.
(2)省钱时y2-y1>0,可得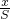 <
<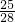 ;对于用电量按时均等的电器,高峰用电时段的时间与总时间的比为
;对于用电量按时均等的电器,高峰用电时段的时间与总时间的比为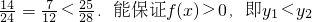 .所以能省钱.
.所以能省钱.
点评:本题考查了与实际生活相关的峰谷用电问题,并通过作差来比较函数值的大小,属于基础题目.
实行峰谷电价的电费为y1=0.56x+(S-x)×0.28=0.28S+0.28x;
现行电价的电费为y2=0.53S;
电费总差额f(x)=y2-y1=0.25S-0.28x,(0≤x≤S)
(2)可以省钱,因为f(x)>0,即0.25S-0.28x>0,∴
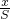 <
<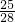 .
.对于用电量按时均等的电器,高峰用电时段的时间与总时间的比为
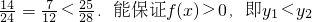 .
.所以用电量按时均等的电器采用峰谷电价的计费方法后能省钱.
分析:(1)总用电量为S千瓦时,高锋时段用电量为x千瓦时,则低谷时段用电量为(S-x)千瓦时;实行峰谷电价的电费y1=0.56x+(S-x)×0.28;现行电价的电费y2=0.53S;作差比较y2-y1即可.
(2)省钱时y2-y1>0,可得
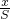 <
<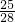 ;对于用电量按时均等的电器,高峰用电时段的时间与总时间的比为
;对于用电量按时均等的电器,高峰用电时段的时间与总时间的比为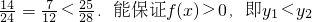 .所以能省钱.
.所以能省钱.点评:本题考查了与实际生活相关的峰谷用电问题,并通过作差来比较函数值的大小,属于基础题目.

练习册系列答案
相关题目