题目内容
已知双曲线C: 的离心率e=
的离心率e= ,其一条准线方程为x=
,其一条准线方程为x= .
.(Ⅰ)求双曲线C的方程;
(Ⅱ)如题20图:设双曲线C的左右焦点分别为A,B,点D为该双曲线右支上一点,直线AD与其左支交于点E,若
 ,求实数λ的取值范围.
,求实数λ的取值范围.
【答案】分析:(I)由题意可得, 可求a,c,由b2=c2-a2可求b,可求双曲线的方程
可求a,c,由b2=c2-a2可求b,可求双曲线的方程
(II)由(I)知A(-2,0),设D(x,y),E(x1,y1)则由 可得
可得 ,
, ,结合E,D在双曲线上,可求x,结合双曲线的性质可求λ
,结合E,D在双曲线上,可求x,结合双曲线的性质可求λ
解答:解(I)由题意可得,
∴
∴双曲线的方程为 (4分)
(4分)
(II)由(I)知A(-2,0),设D(x,y),E(x1,y1)
∴ ,
,
则由
可得 ,
,
∵E在双曲线上
∴
∴
∵D在双曲线
∴
代入上式可得,
∵
∴
∴
∵D在双曲线的左支,点D在右支
∴ (12分)
(12分)
点评:本题主要考查了利用双曲线的性质求解双曲线的方程,双曲线的性质的应用,属于综合试题
 可求a,c,由b2=c2-a2可求b,可求双曲线的方程
可求a,c,由b2=c2-a2可求b,可求双曲线的方程(II)由(I)知A(-2,0),设D(x,y),E(x1,y1)则由
 可得
可得 ,
, ,结合E,D在双曲线上,可求x,结合双曲线的性质可求λ
,结合E,D在双曲线上,可求x,结合双曲线的性质可求λ解答:解(I)由题意可得,

∴

∴双曲线的方程为
 (4分)
(4分)(II)由(I)知A(-2,0),设D(x,y),E(x1,y1)
∴
 ,
,
则由

可得
 ,
,
∵E在双曲线上
∴

∴

∵D在双曲线
∴

代入上式可得,

∵

∴

∴

∵D在双曲线的左支,点D在右支
∴
 (12分)
(12分)点评:本题主要考查了利用双曲线的性质求解双曲线的方程,双曲线的性质的应用,属于综合试题

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知双曲线
-
=1(a>0,b>0),过其左焦点F1作x轴的垂线交双曲线于A、B两点,若双曲线右顶点在以AB为直径的圆内,则双曲线离心离的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(2,+∞) | ||
| B、(1,2) | ||
C、(
| ||
D、(1,
|
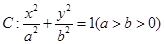 的离心学率为
的离心学率为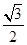 .双曲线
.双曲线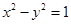 的渐近线与椭圆
的渐近线与椭圆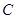 有四个交点,以这四个焦点为顶点的四边形的面积为16,则椭圆
有四个交点,以这四个焦点为顶点的四边形的面积为16,则椭圆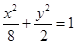 (B)
(B)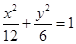
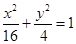 (D)
(D)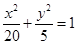
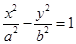 的一条渐近线方程为
的一条渐近线方程为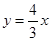 ,则双曲线的离心
,则双曲线的离心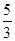 B.
B.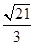 C.
C.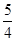 D.
D.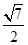
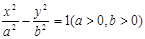 的左、右两焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线的离心e的范围是 ( )
的左、右两焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线的离心e的范围是 ( )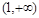 B.
B.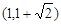 C.
C.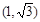 D.
D.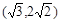
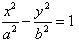 和椭圆
和椭圆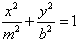 (a>0,m>b>0)的离心离互为倒数,那么以a,b,m为边长的三角形一定是
(a>0,m>b>0)的离心离互为倒数,那么以a,b,m为边长的三角形一定是