题目内容
测得变量x与y的一组数据为：
若这两个变量之间的关系符合回归直线方程
=8.5x+a，则a的值是（ ）
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 30 | 50 | 60 | 70 |
| ? |
| y |
| A、4.5 | B、3.5 |
| C、2.5 | D、1.5 |
分析：先求出这组数据的x和y的平均数，写出这组数据的样本中心点，把样本中心点代入直线的方程，求出a的值．
解答：解：∵
=
=5，
=
=46，
∴这组数据的样本中心点是（5，46）
∴（5，46）满足直线的方程，
∴46=8.5×5+a，
∴a=1.5
故选D．
. |
| x |
| 2+4+5+6+8 |
| 5 |
. |
| y |
| 20+30+50+60+70 |
| 5 |
∴这组数据的样本中心点是（5，46）
∴（5，46）满足直线的方程，
∴46=8.5×5+a，
∴a=1.5
故选D．
点评：本题考查线性回归方程的应用，本题解题的关键是理解样本中心点在线性回归直线上，这是求a的方法，本题是一个基础题．
练习册系列答案
相关题目
，则a的值是
为了研究某灌溉渠道水的流速y与水深x之间的关系，测得一组数据如下表：
（1）画出散点图，判断变量y与x是否具有相关关系；
（2）若y与x之间具有线性相关关系，求y对x的回归直线方程；
（3）预测水深为1.95m水的流速是多少．
| 水深x（m） | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 流速y（m/s） | 1 | 1.5 | 2 | 2.5 | 3 |
（2）若y与x之间具有线性相关关系，求y对x的回归直线方程；
（3）预测水深为1.95m水的流速是多少．
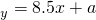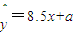，则a的值是（ ）