题目内容
为了研究某灌溉渠道水的流速y与水深x之间的关系,测得一组数据如下表:| 水深x(m) | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 流速y(m/s) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)若y与x之间具有线性相关关系,求y对x的回归直线方程;
(3)预测水深为1.95m水的流速是多少.
【答案】分析:(1)根据散点图可以直观地看出变量y与x之间有近似的线性相关关系;
(2)求出横标和纵标的平均数,写出样本中心点,由回归直线的斜率可求回归直线的方程;
(3)当x=1.95时,代入回归直线方程计算,即可得到水深为1.95m水的流速
解答:解:(1)散点图如图,
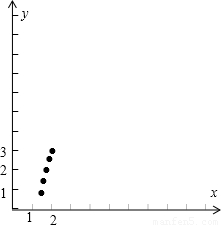 ,具有相关关系.…(2分)
,具有相关关系.…(2分)
(2)经计算可得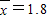 ,
,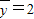 ,
,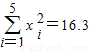 ,
,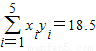 …(4分)
…(4分)
b=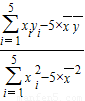 =
=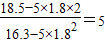 …(6分)
…(6分)
a=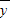 -b
-b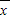 =2-5×1.8=-7.…(7分)
=2-5×1.8=-7.…(7分)
故所求的回归直线方程为y=5x-7.…(8分)
(3)当x=1.95时,y?=5×1.95-7=2.75.即水深为1.95m 时水的流速约是2.75m/s.…(10分)
点评:本题考查线性回归方程,考查线性回归方程的应用,从散点图可以直观地看出变y与x之间有线性相关关系,利用线性回归方程用来预报当自变量取某一个数值时对应的y的值,属于基础题.
(2)求出横标和纵标的平均数,写出样本中心点,由回归直线的斜率可求回归直线的方程;
(3)当x=1.95时,代入回归直线方程计算,即可得到水深为1.95m水的流速
解答:解:(1)散点图如图,
 ,具有相关关系.…(2分)
,具有相关关系.…(2分)(2)经计算可得
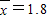 ,
,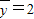 ,
,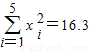 ,
,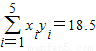 …(4分)
…(4分)b=
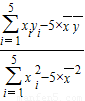 =
=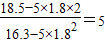 …(6分)
…(6分)a=
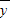 -b
-b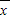 =2-5×1.8=-7.…(7分)
=2-5×1.8=-7.…(7分)故所求的回归直线方程为y=5x-7.…(8分)
(3)当x=1.95时,y?=5×1.95-7=2.75.即水深为1.95m 时水的流速约是2.75m/s.…(10分)
点评:本题考查线性回归方程,考查线性回归方程的应用,从散点图可以直观地看出变y与x之间有线性相关关系,利用线性回归方程用来预报当自变量取某一个数值时对应的y的值,属于基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目