题目内容
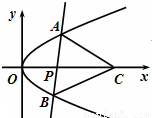
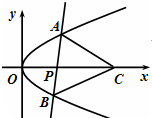 设直线l与抛物线y2=2px(p>0)交于A,B两点,已知当直线l经过抛物线的焦点且与x轴垂直时,△OAB的面积为
设直线l与抛物线y2=2px(p>0)交于A,B两点,已知当直线l经过抛物线的焦点且与x轴垂直时,△OAB的面积为| 1 | 2 |
(1)求抛物线的方程;
(2)当直线l经过点P(a,0)(a>0)且与x轴不垂直时,若在x轴上存在点C,使得△ABC为正三角形,求a的取值范围.
分析:(1)由条件可得|AB|=2p,O点到AB距离为
,结合△OAB的面积为
,即可求得抛物线的方程;
(2)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),设C(t,0),直线l的方程为x=my+a(m≠0),代入y2=2x,可得y0=m,从而x0=m2+a,根据△ABC为正三角形,可得MC⊥AB,|MC|=
|AB|,从而可确定a的取值范围.
| p |
| 2 |
| 1 |
| 2 |
(2)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),设C(t,0),直线l的方程为x=my+a(m≠0),代入y2=2x,可得y0=m,从而x0=m2+a,根据△ABC为正三角形,可得MC⊥AB,|MC|=
| ||
| 2 |
解答:解:(1)由条件可得|AB|=2p,O点到AB距离为
,
∴S△OAB=
×2p×
=
,
∵△OAB的面积为
,∴p=1,
∴抛物线的方程为y2=2x.
(2)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),
又设C(t,0),直线l的方程为x=my+a(m≠0),代入y2=2x得y2-2my-2a=0.
∴△=4(m2+2a),y1+y2=2m,y1y2=-2a.
所以y0=m,从而x0=m2+a.
∵△ABC为正三角形,∴MC⊥AB,|MC|=
|AB|.
由MC⊥AB,得
×
=-1,所以t=m2+a+1.
由|MC|=
|AB|,得
=
×
,
又∵t=m2+a+1,
∴1+m2=3(m2+1)(m2+2a),
从而a=
-
.
∵m≠0,∴m2>0,∴0<a<
.
∴a的取值范围为(0,
).
| p |
| 2 |
∴S△OAB=
| 1 |
| 2 |
| p |
| 2 |
| p2 |
| 2 |
∵△OAB的面积为
| 1 |
| 2 |
∴抛物线的方程为y2=2x.
(2)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),
又设C(t,0),直线l的方程为x=my+a(m≠0),代入y2=2x得y2-2my-2a=0.
∴△=4(m2+2a),y1+y2=2m,y1y2=-2a.
所以y0=m,从而x0=m2+a.
∵△ABC为正三角形,∴MC⊥AB,|MC|=
| ||
| 2 |
由MC⊥AB,得
| y0 |
| x0-t |
| 1 |
| m |
由|MC|=
| ||
| 2 |
| (m2+a-t)2+m2 |
| ||
| 2 |
| (m2+1)×4(m2+2a) |
又∵t=m2+a+1,
∴1+m2=3(m2+1)(m2+2a),
从而a=
| 1 |
| 6 |
| m2 |
| 2 |
∵m≠0,∴m2>0,∴0<a<
| 1 |
| 6 |
∴a的取值范围为(0,
| 1 |
| 6 |
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查学生的计算能力,综合性强.

练习册系列答案
相关题目
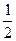 (O为坐标原点).
(O为坐标原点). 轴不垂直时,
轴不垂直时, 点C,使得△ABC为等边三角形,求a
点C,使得△ABC为等边三角形,求a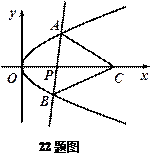
 (O为坐标原点).
(O为坐标原点).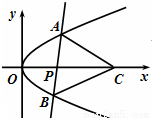
 (O为坐标原点).
(O为坐标原点).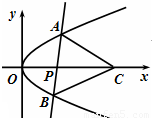
 (O为坐标原点).
(O为坐标原点).