题目内容
下列四个命题：
①满足
=
的复数只有±1，±i；
②若a，b是两个相等的实数，则（a-b）+（a+b）i是纯虚数；
③|z+
|=2|z|；
④复数z∈R的充要条件是z=
；
其中正确的有（ ）
①满足
. |
| z |
| 1 |
| z |
②若a，b是两个相等的实数，则（a-b）+（a+b）i是纯虚数；
③|z+
. |
| z |
④复数z∈R的充要条件是z=
. |
| z |
其中正确的有（ ）
分析：对于①z2=1，可判断错误；对于②找出反例a=b=0不满足题意，判定错误；③若z=i，则其不正确；对于④z=
，则其虚部为0，故正确．故可得答案．
. |
| z |
解答：解：对于①有：z2=1，z=±i，z2=-1，不满足，可判断错误；
②（a-b）+（a+b）i=2ai，∴a=b≠0时，（a-b）+（a+b）i是纯虚数，错误；
③若z=i，则其不正确；
对于④z=
，则其虚部为0，故正确；
故答案为④．
故选B．
②（a-b）+（a+b）i=2ai，∴a=b≠0时，（a-b）+（a+b）i是纯虚数，错误；
③若z=i，则其不正确；
对于④z=
. |
| z |
故答案为④．
故选B．
点评：本题考查复数的基本概念、充要条件、命题的真假判断与应用，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
；⑵
纯虚数； 
；⑷复平面内
轴是实轴，
轴是虚轴，其中正确的结论有（ ）
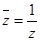的复数只有
1,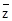
|=2|z|;
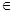R的充要条件是z=
;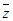