题目内容
在△ABC中,已知c= ,b=1,B=30°.(1)求角A; (2)求△ABC的面积.
,b=1,B=30°.(1)求角A; (2)求△ABC的面积.
(1)A=90°或A=30°; (2) 或
或 .
.
解析试题分析:(1) 先由已知及正弦定理求出角C的正弦函数值,进而求得角C的大小,再由三角形的内角和定理求出角A的大小,注意角C的取值范围及三角函数的多值性,以防漏解;(2)用两边及夹角正弦值积的一半求三角形的面积.
试题解析:(1)由 =
= 得sin C=
得sin C= sin B=
sin B= ×sin 30°=
×sin 30°= .
.
∵c>b,∴C>B,∴C=60°或C=120°.∴A=90°或A=30°.
(2)S△ABC= bcsin A=
bcsin A= ×1×sin 90°=
×1×sin 90°= .
.
或S△ABC= bcsin A=
bcsin A= ×1×
×1× ×sin 30°=
×sin 30°= .即△ABC的面积为
.即△ABC的面积为 或
或 .
.
考点:1.正弦定理;2.三角形的面积.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小. ,并在点C测得塔顶A的仰角为
,并在点C测得塔顶A的仰角为 ,求塔高AB.
,求塔高AB.
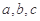 ,且,,.
,且,,. 的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.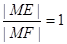 时,试问x的值为多少?(2)求
时,试问x的值为多少?(2)求 的取值范围.
的取值范围. 、
、 、
、 分别为
分别为 的三边
的三边 、
、 、
、 所对的角,向量
所对的角,向量 ,
, ,且
,且 .
. ,求边
,求边 的三个内角
的三个内角 所对的边分别为
所对的边分别为
 ,若
,若 ,
, .
.