题目内容
已知定点A(0,1)、B(0,-1)、C(1,0),动点P满足 ·
· =k|
=k| |2.
|2.
(1) 求动点P的轨迹方程,并说明方程表示的曲线.
(2) 当k=2时,求|2 +
+ |的最大值和最小值
|的最大值和最小值
【答案】
(1)设动点的坐标为P(x,y),则
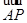 =(x,y-1),
=(x,y-1),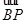 =(x,y+1),
=(x,y+1), =(1-x,-y).
=(1-x,-y).
∵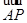 ·
·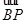 =k|
=k| |2, ∴x2+y2-1=k[(x-1)2+y2], ∴(1-k)x2+(1-k)y2+2kx-k-1=0.
|2, ∴x2+y2-1=k[(x-1)2+y2], ∴(1-k)x2+(1-k)y2+2kx-k-1=0.
若k=1,则方程为x=1,表示过点(1,0)且平行于y轴的直线.
若k≠1,则方程化为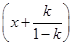 2+y2=
2+y2= 2,
2,
表示以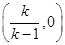 为圆心,以
为圆心,以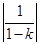 为半径的圆.
为半径的圆.
(2)当k=2时,方程化为(x-2)2+y2=1.
∵2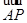 +
+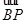 =2(x,y-1)+(x,y+1)=(3x,3y-1),
=2(x,y-1)+(x,y+1)=(3x,3y-1),
∴|2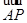 +
+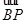 |=
|=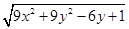 =
=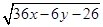 .
.
又∵(x-2)2+y2=1,则令x=2+cosθ,y=sinθ,
于是有36x-6y-26=36cosθ-6sinθ+46=6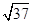 cos(θ+φ)+46∈[46-6
cos(θ+φ)+46∈[46-6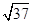 ,46+6
,46+6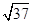 ],
],
故|2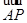 +
+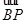 |的最大值为
|的最大值为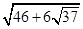 =3+
=3+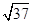 ,最小值为
,最小值为 =
=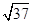 -3
-3
【解析】略

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目