题目内容
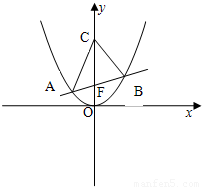
设直线l过抛物线x2=2py(p>0)的焦点F,且与该抛物线交于A、B两点,l的斜率为k,点C(0,t),当k=0,t=1+2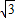 时,△ABC为等边三角形.
时,△ABC为等边三角形.(Ⅰ)求抛物线的方程.
(Ⅱ)若不论实数k取何值,∠ACB始终为钝角,求实数t的取值范围.
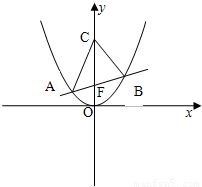
【答案】分析:(1)直线l过抛物线x2=2py(p>0)的焦点F,l的斜率为k,知直线l的方程为:y=kx+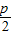 ,当k=0时,y=
,当k=0时,y=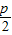 ,C(0,1+2
,C(0,1+2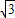 ),CF=1+2
),CF=1+2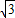 -
- ,AB=2p,由此利用△ABC是等边三角形,能求出抛物线的方程.
,AB=2p,由此利用△ABC是等边三角形,能求出抛物线的方程.
(2)由(1)知,抛物线的方程为x2=4y,直线l的方程为:y=kx+1,联立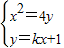 ,得x2-4kx-4=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4,由C(0,t),知
,得x2-4kx-4=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4,由C(0,t),知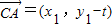 ,
,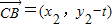 ,由不论实数k取何值,∠ACB始终为钝角,知
,由不论实数k取何值,∠ACB始终为钝角,知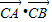 =x1x2+(y1-t)(y2-t)<0,由此能求出实数t的取值范围.
=x1x2+(y1-t)(y2-t)<0,由此能求出实数t的取值范围.
解答:解:(1)∵直线l过抛物线x2=2py(p>0)的焦点F,l的斜率为k,
∴直线l的方程为:y=kx+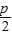 ,
,
当k=0时,y=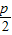 ,C(0,1+2
,C(0,1+2 ),CF=1+2
),CF=1+2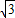 -
- ,AB=2p,
,AB=2p,
∵△ABC是等边三角形,
∴4p2-p2=(1+2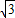 -
-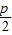 )2,解得p=2.
)2,解得p=2.
∴抛物线的方程为x2=4y.
(2)由(1)知,抛物线的方程为x2=4y,直线l的方程为:y=kx+1,
联立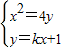 ,得x2-4kx-4=0,
,得x2-4kx-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4,
∴y1y2=(kx1+1)•(kx2+1)=k2x1x2+k(x1+x2)+1=-4k2+4k2+1=1,
y1+y2=(kx1+1)+(kx2+1)=k(x1+x2)+2=4k2+2,
∵C(0,t),∴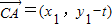 ,
,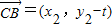 ,
,
∵不论实数k取何值,∠ACB始终为钝角,
∴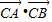 <0,
<0,
∴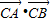 =x1x2+(y1-t)(y2-t)
=x1x2+(y1-t)(y2-t)
=x1x2+y1y2-t(y1+y2)+t2
=-4+1-4k2t-2t+t2
=t2-(4k2+2)t-3<0.
∴以k为自变量的不等式4tk2+2t-t2+3>0的解集是R,
∴t=0,或 ,
,
即t=0,或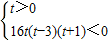 ,
,
解得0≤t<3.
∴实数t的取值范围是[0,3).
点评:本题考查抛物线的方程的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
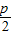 ,当k=0时,y=
,当k=0时,y=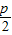 ,C(0,1+2
,C(0,1+2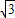 ),CF=1+2
),CF=1+2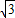 -
- ,AB=2p,由此利用△ABC是等边三角形,能求出抛物线的方程.
,AB=2p,由此利用△ABC是等边三角形,能求出抛物线的方程.(2)由(1)知,抛物线的方程为x2=4y,直线l的方程为:y=kx+1,联立
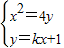 ,得x2-4kx-4=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4,由C(0,t),知
,得x2-4kx-4=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4,由C(0,t),知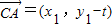 ,
,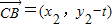 ,由不论实数k取何值,∠ACB始终为钝角,知
,由不论实数k取何值,∠ACB始终为钝角,知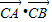 =x1x2+(y1-t)(y2-t)<0,由此能求出实数t的取值范围.
=x1x2+(y1-t)(y2-t)<0,由此能求出实数t的取值范围.解答:解:(1)∵直线l过抛物线x2=2py(p>0)的焦点F,l的斜率为k,
∴直线l的方程为:y=kx+
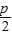 ,
,当k=0时,y=
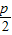 ,C(0,1+2
,C(0,1+2 ),CF=1+2
),CF=1+2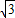 -
- ,AB=2p,
,AB=2p,∵△ABC是等边三角形,
∴4p2-p2=(1+2
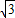 -
-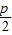 )2,解得p=2.
)2,解得p=2.∴抛物线的方程为x2=4y.
(2)由(1)知,抛物线的方程为x2=4y,直线l的方程为:y=kx+1,
联立
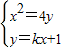 ,得x2-4kx-4=0,
,得x2-4kx-4=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4,
∴y1y2=(kx1+1)•(kx2+1)=k2x1x2+k(x1+x2)+1=-4k2+4k2+1=1,
y1+y2=(kx1+1)+(kx2+1)=k(x1+x2)+2=4k2+2,
∵C(0,t),∴
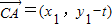 ,
,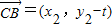 ,
,∵不论实数k取何值,∠ACB始终为钝角,
∴
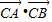 <0,
<0,∴
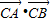 =x1x2+(y1-t)(y2-t)
=x1x2+(y1-t)(y2-t)=x1x2+y1y2-t(y1+y2)+t2
=-4+1-4k2t-2t+t2
=t2-(4k2+2)t-3<0.
∴以k为自变量的不等式4tk2+2t-t2+3>0的解集是R,
∴t=0,或
 ,
,即t=0,或
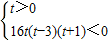 ,
,解得0≤t<3.
∴实数t的取值范围是[0,3).
点评:本题考查抛物线的方程的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
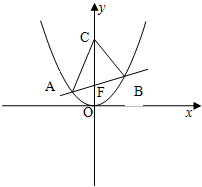 设直线l过抛物线x2=2py(p>0)的焦点F,且与该抛物线交于A、B两点,l的斜率为k,点C(0,t),当k=0,t=1+2
设直线l过抛物线x2=2py(p>0)的焦点F,且与该抛物线交于A、B两点,l的斜率为k,点C(0,t),当k=0,t=1+2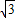 时,△ABC为等边三角形.
时,△ABC为等边三角形.