Question

某赛季足球比赛的计分规则是：胜一场，得3分；平一场得1分；负一场是0分.一球队打完15场，积33分.若不考虑顺序，该队胜、负、平的情形共有(    )

A.3种          B.4种              C.5种               D.6种

Answer 1

解析：设该队胜x场，平y场，负z场，则x,y,z是非负整数，且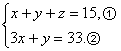因为不考虑胜、平、负的顺序，所以问题转化为求此方程组的不同非负整数解的组数.

由②得，y=3(11-x),代入①式，得z=2(x-9).由0≤y≤15,0≤z≤15，可知因为x是非负整数,所以这个不等式组的解为9≤x≤11,即x最多只能取9,10,11三个值,对应的y值也只能取6,3,0三个值,对应的z值也只能取0,2,4三个值.从而①②组成的方程组有且只有三组的非负整数解,选A.