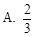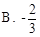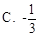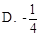题目内容
设平面向量
=(
sinx,2cosx),
=(2sin(
-x),cosx),已知f(x)=
•
+m在[0,
]上的最大值为6.
(Ⅰ)求实数m的值;
(Ⅱ)若f(
+x0)=
,x0∈[
,
].求cos2x0的值.
| a |
| 3 |
| b |
| π |
| 2 |
| a |
| b |
| π |
| 2 |
(Ⅰ)求实数m的值;
(Ⅱ)若f(
| π |
| 2 |
| 14 |
| 5 |
| π |
| 4 |
| π |
| 2 |
(Ⅰ)f(x)=
•
+m=
sinx•2sin(
-x)+2cos2x+m=
sin2x+cos2x+1+m=2sin(2x+
)+1+m,
∵x∈[0,
],2x+
∈[
,
],
∴2sin(2x+
)∈[-
,1],
∴f(x)max=2+1+m=6,
∴m=3;
(Ⅱ)∵f(x)=2sin(2x+
)+4,
∴f(
+x0)=2sin[2(
+x0)+
]+4=
,
即sin(2x0+
)=
,
∵x0∈[
,
],
∴2x0+
∈[
,
],
∴cos(2x0+
)<0,
∴cos(2x0+
)=-
,
则cos2x0=cos[(2x0+
)-
]=
cos(2x0+
)+
sin(2x0+
)=-
×
+
×
=
.
| a |
| b |
| 3 |
| π |
| 2 |
| 3 |
| π |
| 6 |
∵x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴2sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∴f(x)max=2+1+m=6,
∴m=3;
(Ⅱ)∵f(x)=2sin(2x+
| π |
| 6 |
∴f(
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 14 |
| 5 |
即sin(2x0+
| π |
| 6 |
| 3 |
| 5 |
∵x0∈[
| π |
| 4 |
| π |
| 2 |
∴2x0+
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
∴cos(2x0+
| π |
| 6 |
∴cos(2x0+
| π |
| 6 |
| 4 |
| 5 |
则cos2x0=cos[(2x0+
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 4 |
| 5 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
3-4
| ||
| 10 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
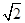 cosx(m>0)的最大值为2.
cosx(m>0)的最大值为2. 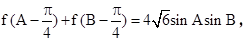 角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.
角A,B,C所对的边分别是a,b,c, 且C=60°,c=3,求△ABC的面积.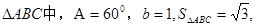 则
则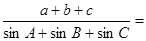 ( )
( )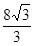
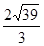
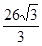
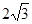
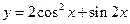 的最小值是____________________ .
的最小值是____________________ .
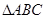 中,角
中,角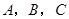 所对的边分别为
所对的边分别为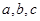 ,角
,角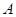 为锐角,且
为锐角,且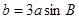 ,则
,则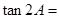 .
.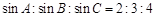 ,那cosC等于 ( ).
,那cosC等于 ( ).