题目内容
(本题满分14分)
在△ABC中,角A,B,C所对的边为a,b,c,已知sin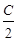 =
=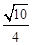 .
.
(Ⅰ) 求cos C的值;
(Ⅱ) 若△ABC的面积为 ,且sin2 A+sin2B=
,且sin2 A+sin2B=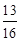 sin2 C,求c的值.
sin2 C,求c的值.
在△ABC中,角A,B,C所对的边为a,b,c,已知sin
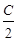 =
=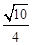 .
.(Ⅰ) 求cos C的值;
(Ⅱ) 若△ABC的面积为
 ,且sin2 A+sin2B=
,且sin2 A+sin2B=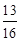 sin2 C,求c的值.
sin2 C,求c的值.(Ⅰ) 解:因为sin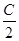 =
=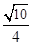 ,
,
所以cos C=1- 2sin2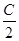 =
=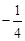 . …………4分
. …………4分
(Ⅱ) 解:因为sin2 A+sin2B=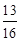 sin2 C,由正弦定理得
sin2 C,由正弦定理得
a2+b2=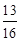 c2.-------① …………6分
c2.-------① …………6分
由余弦定理得a2+b2=c2+2abcos C,将cos C=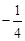 代入,得
代入,得
ab=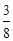 c2.--------② …………8分
c2.--------② …………8分
由S△ABC= 及sin C=
及sin C=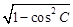 =
=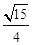 ,得
,得
ab=6.----------③ …………12分
所以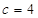 …………14分
…………14分
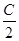 =
=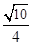 ,
,所以cos C=1- 2sin2
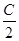 =
=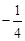 . …………4分
. …………4分(Ⅱ) 解:因为sin2 A+sin2B=
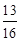 sin2 C,由正弦定理得
sin2 C,由正弦定理得a2+b2=
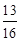 c2.-------① …………6分
c2.-------① …………6分由余弦定理得a2+b2=c2+2abcos C,将cos C=
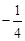 代入,得
代入,得ab=
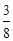 c2.--------② …………8分
c2.--------② …………8分由S△ABC=
 及sin C=
及sin C=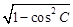 =
=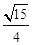 ,得
,得ab=6.----------③ …………12分
所以
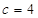 …………14分
…………14分略

练习册系列答案
相关题目
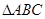 中,
中,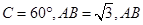 边上的高为
边上的高为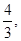 则
则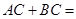
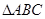 中,
中,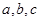 分别是角
分别是角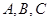 的对边,且
的对边,且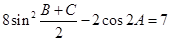 ,则
,则 ______.
______.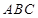 的内角
的内角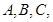 的对边分别为
的对边分别为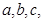
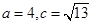 ,
,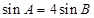 .
.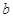 边的长;
边的长;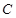 的大小.
的大小.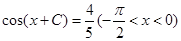 ,求
,求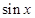 .
.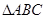 中,已知
中,已知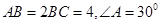 ,则
,则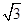
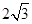
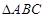 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为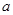 、
、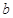 、
、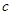 ,已知
,已知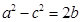 ,且
,且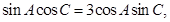 求b=
求b= 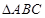 的三个内角,则下列各式中化简结果一定是0的是( )
的三个内角,则下列各式中化简结果一定是0的是( )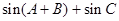
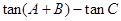
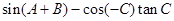
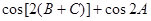
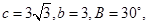 此三角形的解的情况是( )
此三角形的解的情况是( )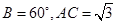 ,则
,则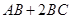 的最大值为
的最大值为