题目内容
20.设空间两个单位向量$\overrightarrow{OA}$=(m,n,0),$\overrightarrow{OB}$=(0,n,p)与向量$\overrightarrow{OC}$=(1,1,1)的夹角都等于$\frac{π}{4}$,求cos∠AOB的值.分析 由已知得$\overrightarrow{OC}•\overrightarrow{OA}$=|$\overrightarrow{OC}$|$•|\overrightarrow{OA}|$$•cos\frac{π}{4}$=$\sqrt{3}×1×\frac{\sqrt{2}}{2}=\frac{\sqrt{6}}{2}$=m+n,${\overrightarrow{OA}}^{2}={m}^{2}+{n}^{2}=1$,由此能求出n2,再由cos∠AOB=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=n2,能求出cos∠AOB.
解答 解:∵两个单位向量$\overrightarrow{OA}$=(m,n,0),$\overrightarrow{OB}$=(0,n,p)与向量$\overrightarrow{OC}$=(1,1,1)的夹角都等于$\frac{π}{4}$,
∴$∠AOC=∠BOC=\frac{π}{4}$,|$\overrightarrow{OC}$|=$\sqrt{3}$,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,
∴$\overrightarrow{OC}•\overrightarrow{OA}$=|$\overrightarrow{OC}$|$•|\overrightarrow{OA}|$$•cos\frac{π}{4}$=$\sqrt{3}×1×\frac{\sqrt{2}}{2}=\frac{\sqrt{6}}{2}$,
∵$\overrightarrow{OC}•\overrightarrow{OA}$=m+n,${\overrightarrow{OA}}^{2}={m}^{2}+{n}^{2}=1$,
∴$\left\{\begin{array}{l}{m+n=\frac{\sqrt{6}}{2}}\\{{m}^{2}+{n}^{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{m}^{2}=\frac{2+\sqrt{3}}{4}}\\{{n}^{2}=\frac{2-\sqrt{3}}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{{m}^{2}=\frac{2-\sqrt{3}}{4}}\\{{n}^{2}=\frac{2+\sqrt{3}}{4}}\end{array}\right.$,
∵$\overrightarrow{OA}•\overrightarrow{OB}$=n2,
∴cos∠AOB=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=n2,
∴cos∠AOB=$\frac{2+\sqrt{3}}{4}$或cos∠AOB=$\frac{2-\sqrt{3}}{4}$.
点评 本题考查角的余弦值的求法,是中档题,解题时要认真审题,注意向量的数量积、向理夹角余弦值的坐标运算公式的合理运用.

 阅读快车系列答案
阅读快车系列答案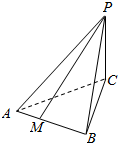 已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )
已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )| A. | 2$\sqrt{43}$ | B. | $\sqrt{43}$ | C. | $\sqrt{11}$ | D. | 2$\sqrt{11}$ |
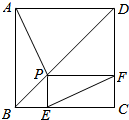 如图所示,P是正方形ABCD对角线BD上一点,四边形PECF是矩形,求证:
如图所示,P是正方形ABCD对角线BD上一点,四边形PECF是矩形,求证: