题目内容
有编号为1,2,3的三个白球,编号为4,5,6的三个黑球,这六个球除编号和颜色外完全相同,现从中任意取出两个球.
(1)求取得的两个球颜色相同的概率;
(2)求取得的两个球颜色不相同的概率.
(1)求取得的两个球颜色相同的概率;
(2)求取得的两个球颜色不相同的概率.
(1)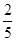 (2)
(2)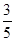
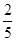 (2)
(2)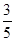
从六个球中取出两个球的基本事件:
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共计15个基本事件.
(1)记事件A为取出的两个球是白球,则这个事件包含的基本事件是(1,2),(1,3),(2,3),共计3个基本事件,故P(A)=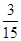 =
=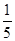 .
.
记取出的两个球是黑球为事件B,同理可得P(B)=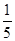 .
.
记事件C为取出的两个球的颜色相同,则C=A+B,且A,B互斥,根据互斥事件的概率加法公式,得P(C)=P(A+B)=P(A)+P(B)=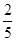 .
.
(2)记事件D为取出的两个球的颜色不相同,则事件C,D互斥,根据互斥事件概率之间的关系,得P(D)=1-P(C)=1-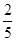 =
=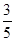 .
.
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共计15个基本事件.
(1)记事件A为取出的两个球是白球,则这个事件包含的基本事件是(1,2),(1,3),(2,3),共计3个基本事件,故P(A)=
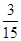 =
=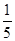 .
.记取出的两个球是黑球为事件B,同理可得P(B)=
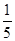 .
.记事件C为取出的两个球的颜色相同,则C=A+B,且A,B互斥,根据互斥事件的概率加法公式,得P(C)=P(A+B)=P(A)+P(B)=
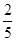 .
.(2)记事件D为取出的两个球的颜色不相同,则事件C,D互斥,根据互斥事件概率之间的关系,得P(D)=1-P(C)=1-
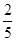 =
=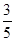 .
.
练习册系列答案
相关题目
 中随机取出一个数,设事件
中随机取出一个数,设事件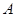 为“取出的数是偶数”, 事件
为“取出的数是偶数”, 事件 为“取出的数是奇数”,则事件
为“取出的数是奇数”,则事件 ,
, ,则
,则 等于( ).
等于( ).