题目内容
已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小;
(3)求证:二面角B—PC—D为直二面角.

(1)![]() (2) PC与BD所成角的余弦值为
(2) PC与BD所成角的余弦值为![]() (3)证明略
(3)证明略
解析:
因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB=![]() .
.
∴PC=![]() .
.
(2)解: 如图,过点C作CE∥BD交AD的延长线于E,连结PE,则PC与BD所成的角为∠PCE或它的补角.

∵CE=BD=![]() ,且PE=
,且PE=![]()
∴由余弦定理得
cosPCE=![]()
∴PC与BD所成角的余弦值为![]() .
.
(3)证明:设PB、PC中点分别为G、F,连结FG、AG、DF,

则GF∥BC∥AD,且GF=![]() BC=1=AD,
BC=1=AD,
从而四边形ADFG为平行四边形,
又AD⊥平面PAB,∴AD⊥AG,
即ADFG为矩形,DF⊥FG.
在△PCD中,PD=![]() ,CD=
,CD=![]() ,F为BC中点,
,F为BC中点,
∴DF⊥PC
从而DF⊥平面PBC,故平面PDC⊥平面PBC,
即二面角B—PC—D为直二面角.?
另法(向量法): (略)


练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,已知四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,已知四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.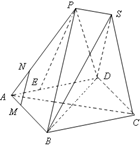 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD. 已知四边形ABCD为直角梯形,∠ADC=90°,AD∥BC,△ABD为等腰直角三角形,平面PAD⊥平面ABCD,E为PA的中点,AD=2BC=
已知四边形ABCD为直角梯形,∠ADC=90°,AD∥BC,△ABD为等腰直角三角形,平面PAD⊥平面ABCD,E为PA的中点,AD=2BC=