题目内容
三位同学合作学习,对问题“已知不等式xy≤ax2+2y2对于x∈[1,2],y∈[2,3]恒成立,求a的取值范围”提出了各自的解题思路.
甲说:“可视x为变量,y为常量来分析”.
乙说:“寻找x与y的关系,再作分析”.
丙说:“把字母a单独放在一边,再作分析”.
参考上述思路,或自已的其它解法,可求出实数a的取值范围是
- A.[-1,6]
- B.[-1,4)
- C.[-1,+∞)
- D.[1,+∞)
C
分析:利用丙的方法,将字母a分离出来,然后将 看成整体,转化成关于
看成整体,转化成关于 的二次函数,求出
的二次函数,求出 的范围,只需研究二次函数在闭区间上的最大值即可.
的范围,只需研究二次函数在闭区间上的最大值即可.
解答: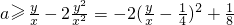 ,
,
又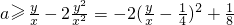 ,
,
而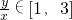 ,
, =-1,
=-1,
故选C.
点评:本题主要考查了函数恒成立的问题,以及参数分离法的运用和转化的数学思想,属于基础题.
分析:利用丙的方法,将字母a分离出来,然后将
 看成整体,转化成关于
看成整体,转化成关于 的二次函数,求出
的二次函数,求出 的范围,只需研究二次函数在闭区间上的最大值即可.
的范围,只需研究二次函数在闭区间上的最大值即可.解答:
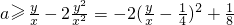 ,
,又
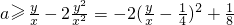 ,
,而
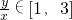 ,
, =-1,
=-1,故选C.
点评:本题主要考查了函数恒成立的问题,以及参数分离法的运用和转化的数学思想,属于基础题.

练习册系列答案
相关题目
 对于
对于 恒成立,求a的取值范围”提出了各自的解题思路.
恒成立,求a的取值范围”提出了各自的解题思路. 为变量,
为变量, 为常量来分析”.
为常量来分析”. 单独放在一边,再作分析”.
单独放在一边,再作分析”. B.
B. C.
C. D.
D.
 对于
对于 恒成立,求
恒成立,求 的取值范围”提出了各自的解题思路.
的取值范围”提出了各自的解题思路. 为变量,
为变量, 为常量来分析”.
为常量来分析”.