题目内容
 如图,目标函数z=kx+y的可行域为四边形OABC(含边界),A(1,0)、C(0,1),若B(
如图,目标函数z=kx+y的可行域为四边形OABC(含边界),A(1,0)、C(0,1),若B(| 3 |
| 4 |
| 2 |
| 3 |
分析:根据已知的可行域,再用角点法分析,若目标函数z=kx+y只在点D处取得最优解,则直线z=kx+y与可行域只有一个交点,即求出实数k的取值范围.
解答:解:直线z=kx+y的斜率为-k,
若目标函数z=kx+y只在点B处取得最优解,
则取得最优解时过B的直线z=kx+y与可行域只有一个交点,
即-KAB<-k<KBC
又∵KAB=-
,KBC=-
,
∴-
<k<-
,⇒
<k<
故选:A.
若目标函数z=kx+y只在点B处取得最优解,
则取得最优解时过B的直线z=kx+y与可行域只有一个交点,
即-KAB<-k<KBC
又∵KAB=-
| 8 |
| 3 |
| 4 |
| 9 |
∴-
| 8 |
| 3 |
| 4 |
| 9 |
| 4 |
| 9 |
| 8 |
| 3 |
故选:A.
点评:图解法解决线性规划问题时,若目标函数z=ax+y只在点D处取得最优解,则过点D线z=ax+y与可行域只有一个交点,由此不难给出直线斜率-a的范围,进一步给出a的范围,但在解题时要注意,区分目标函数是取最大值,还是最小值,这也是这种题型最容易出错的地方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点A处取得最大值,则k的取值范围是
如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点A处取得最大值,则k的取值范围是 (2008•湖北模拟)如图,目标函数z=kx+y的可行域为四边形OABC(含边界),A(1,0)、C(0,1),若
(2008•湖北模拟)如图,目标函数z=kx+y的可行域为四边形OABC(含边界),A(1,0)、C(0,1),若 如图,目标函数z=kx+y的可行域为四边形OABC(含边界),A(1,0)、C(0,1),若
如图,目标函数z=kx+y的可行域为四边形OABC(含边界),A(1,0)、C(0,1),若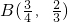 为目标函数取最大值时的最优解,则k的取值范围是
为目标函数取最大值时的最优解,则k的取值范围是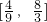
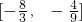
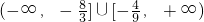
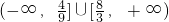
 为目标函数取最大值的最优解,则k的取值范围是 .
为目标函数取最大值的最优解,则k的取值范围是 .