题目内容
有一棱长为a的正方体框架，其内放置一气球，是其充气且尽可能地膨胀（仍保持为球的形状），则气球表面积的最大值为
- A.πa2
- B.2πa2
- C.3πa2
- D.4πa2
B
分析：由题意气球充气且尽可能地膨胀（仍保持为球的形状），与棱长为a的正方体框架相切，球的半径就是正方体面对角线的一半．求出半径，即可求出球的表面积．
解答：气球充气且尽可能地膨胀（仍保持为球的形状），与棱长为a的正方体框架相切，球的半径就是正方体面对角线的一半．
所以球的直径为：
a，半径为：
气球表面积的最大值：4πr2=2πa2
故选B．
点评：本题考查球的表面积，考查计算能力，逻辑思维能力，是基础题．
分析：由题意气球充气且尽可能地膨胀（仍保持为球的形状），与棱长为a的正方体框架相切，球的半径就是正方体面对角线的一半．求出半径，即可求出球的表面积．
解答：气球充气且尽可能地膨胀（仍保持为球的形状），与棱长为a的正方体框架相切，球的半径就是正方体面对角线的一半．
所以球的直径为：
a，半径为：气球表面积的最大值：4πr2=2πa2
故选B．
点评：本题考查球的表面积，考查计算能力，逻辑思维能力，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
有一棱长为a的正方体框架，其内放置一气球，是其充气且尽可能地膨胀（仍保持为球的形状），则气球表面积的最大值为（ ）
| A、πa2 | B、2πa2 | C、3πa2 | D、4πa2 |
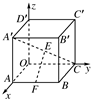如图所示，在空间直角坐标系中，有一棱长为a的正方体ABCO-A′B′C′D′，A′C的中点E与AB的中点F的距离为（ ）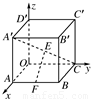
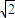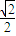a
a
a