题目内容
4.某学校高一、高二、高三三个年级学生人数分别为2000人,1500人,1000人,用分层抽样的方法,从该校三个年级的学生中抽取9人,现将这9人分配到甲、乙两个工厂参观,要求每个工厂每个年级至少去一人,则共有168种不同的分配方案(用数字作答).分析 求出高一、高二、高三三个年级学生人数分别为4,3,2,再分类讨论,利用组合知识,即可得出结论.
解答 解:由题意,用分层抽样的方法,高一、高二、高三三个年级学生人数分别为4,3,2,
因为要求每个工厂每个年级至少去一人,
所以从高一的4人中选一个,从高二3人中分别选1人、2人,从高三的2人中任选1人进甲工厂参观,其余的进乙厂参观,有${C}_{4}^{1}$(${C}_{3}^{1}$+${C}_{3}^{2}$)•${C}_{2}^{1}$=48种方法;
同理可得,从高一的4人中选2个,从高二3人中分别选1人、2人,从高三的2人中任选1人进甲工厂参观,其余的进乙厂参观,有${C}_{4}^{2}$(${C}_{3}^{1}$+${C}_{3}^{2}$)•${C}_{2}^{1}$=72种方法;
从高一的4人中选3个,从高二3人中分别选1人、2人,从高三的2人中任选1人进甲工厂参观,其余的进乙厂参观,有${C}_{4}^{3}$(${C}_{3}^{1}$+${C}_{3}^{2}$)•${C}_{2}^{1}$=48种方法
故答案为:168.
点评 本题考查分层抽样,考查组合知识,考查分类讨论是数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设m∈R,过定点A的动直线mx+y-1=0与过定点B的动直线x-my+m+2=0交于点P(x,y),则|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|的
最大值为( )
最大值为( )
| A. | 2 | B. | $\sqrt{2}$+1 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$+2 |
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N. ,其中
,其中 .
. 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值; (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数 的取值范围.
的取值范围. ,则
,则 ______.
______. .
. 时,求函数
时,求函数 的最大值;
的最大值; 与
与 轴交于两点
轴交于两点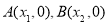 且
且 ,证明:
,证明: .
.