题目内容
已知椭圆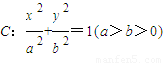 的左顶点为A,右焦点为F,且过点(1,
的左顶点为A,右焦点为F,且过点(1, ),椭圆C的焦点与曲线
),椭圆C的焦点与曲线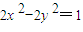 的焦点重合.
的焦点重合.(1)求椭圆C的方程;
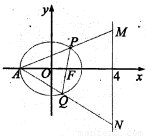
(2)过点F任作椭圆C的一条弦PQ,直线AP、AQ分别交直线x=4于M、N两点,点M、N的纵坐标分别为m、n.请问以线段MN为直径的圆是否经过x轴上的定点?若存在,求出定意的坐标,并证明你的结论;若不存在,请说明理由.
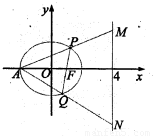
【答案】分析:(1)由题意,椭圆C的焦点为(-1,0),(1,0),且过点(1, ),由椭圆的定义,可得a的值,从而可求椭圆C的方程;
),由椭圆的定义,可得a的值,从而可求椭圆C的方程;
(2)假设以线段MN为直径的圆经过x轴上的定点,由(1)知F(1,0),分类讨论:①当PQ⊥x轴时,以线段MN为直径的圆的方程为(x-4)2+y2=9,可得以线段MN为直径的圆经过x轴上的定点(1,0),(7,0);②当直线PQ与x轴不垂直时,可得以线段MN为直径的圆的方程为(x-4)2+(y- )2=
)2=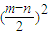 ,验证(1,0),(7,0)在圆上
,验证(1,0),(7,0)在圆上
解答:解:(1)由题意,椭圆C的焦点为(-1,0),(1,0),且过点(1, ),
),
由椭圆的定义,可得2a=4,∴a=2
∴b2=a2-1=3
∴椭圆C的方程为 ;
;
(2)假设以线段MN为直径的圆经过x轴上的定点,由(1)知F(1,0)
①当PQ⊥x轴时,P,Q的横坐标均为1,将x=1代入椭圆方程可得y=±
不妨令P(1, ),Q(1,-
),Q(1,- )
)
由A,P,M三点共线,得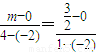 ,∴m=3
,∴m=3
同理可得n=-3
∴以线段MN为直径的圆的方程为(x-4)2+y2=9
令y=0,可得x=1或x=7
∴以线段MN为直径的圆经过x轴上的定点(1,0),(7,0);
②当直线PQ与x轴不垂直时,∵A(-2,0),M(4,m),∴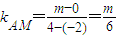
∴直线AM的方程为y=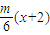
代入椭圆方程,整理可得(27+m2)x2+4m2x+4m2-108=0
设P(x1,y1),Q(x2,y2),则-2与x1是上述方程的两个实根
∴-2x1= ,∴x1=
,∴x1=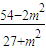 ,∴y1=
,∴y1=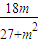
∴P(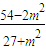 ,
, )
)
同理可得Q(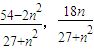 )
)
∴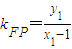 =
= ,
, =
=
∵P,F,Q三点共线,∴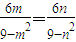
∴(m-n)(9+mn)=0
∵m≠n,∴9+mn=0,∴mn=-9
∴以线段MN为直径的圆的方程为(x-4)2+(y- )2=
)2=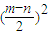
将(1,0)代入上式的坐标,可得(1-4)2+(0-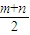 )2=-mn++(
)2=-mn++(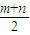 )2=
)2=
∴以线段MN为直径的圆的方程经过点(1,0)
同理(7,0)也在圆上,
综上,以线段MN为直径的圆经过x轴上的定点(1,0),(7,0).
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查恒过定点问题,考查分类讨论的数学思想,综合性强.
 ),由椭圆的定义,可得a的值,从而可求椭圆C的方程;
),由椭圆的定义,可得a的值,从而可求椭圆C的方程;(2)假设以线段MN为直径的圆经过x轴上的定点,由(1)知F(1,0),分类讨论:①当PQ⊥x轴时,以线段MN为直径的圆的方程为(x-4)2+y2=9,可得以线段MN为直径的圆经过x轴上的定点(1,0),(7,0);②当直线PQ与x轴不垂直时,可得以线段MN为直径的圆的方程为(x-4)2+(y-
 )2=
)2=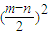 ,验证(1,0),(7,0)在圆上
,验证(1,0),(7,0)在圆上解答:解:(1)由题意,椭圆C的焦点为(-1,0),(1,0),且过点(1,
 ),
),由椭圆的定义,可得2a=4,∴a=2
∴b2=a2-1=3
∴椭圆C的方程为
 ;
;(2)假设以线段MN为直径的圆经过x轴上的定点,由(1)知F(1,0)
①当PQ⊥x轴时,P,Q的横坐标均为1,将x=1代入椭圆方程可得y=±

不妨令P(1,
 ),Q(1,-
),Q(1,- )
)由A,P,M三点共线,得
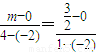 ,∴m=3
,∴m=3同理可得n=-3
∴以线段MN为直径的圆的方程为(x-4)2+y2=9
令y=0,可得x=1或x=7
∴以线段MN为直径的圆经过x轴上的定点(1,0),(7,0);
②当直线PQ与x轴不垂直时,∵A(-2,0),M(4,m),∴
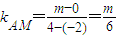
∴直线AM的方程为y=
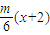
代入椭圆方程,整理可得(27+m2)x2+4m2x+4m2-108=0
设P(x1,y1),Q(x2,y2),则-2与x1是上述方程的两个实根
∴-2x1=
 ,∴x1=
,∴x1=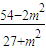 ,∴y1=
,∴y1=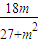
∴P(
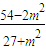 ,
, )
)同理可得Q(
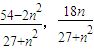 )
)∴
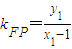 =
= ,
, =
=
∵P,F,Q三点共线,∴
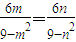
∴(m-n)(9+mn)=0
∵m≠n,∴9+mn=0,∴mn=-9
∴以线段MN为直径的圆的方程为(x-4)2+(y-
 )2=
)2=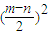
将(1,0)代入上式的坐标,可得(1-4)2+(0-
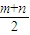 )2=-mn++(
)2=-mn++(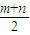 )2=
)2=
∴以线段MN为直径的圆的方程经过点(1,0)
同理(7,0)也在圆上,
综上,以线段MN为直径的圆经过x轴上的定点(1,0),(7,0).
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查恒过定点问题,考查分类讨论的数学思想,综合性强.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
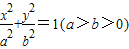 的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若
的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若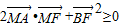 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .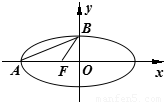 如图,已知椭圆
如图,已知椭圆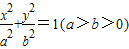 的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .
的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 . 如图,已知椭圆
如图,已知椭圆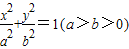 的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .
的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .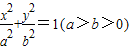 的左顶点为A,左、右焦点分别为F1,F2,且圆C:
的左顶点为A,左、右焦点分别为F1,F2,且圆C: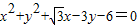 过A,F2两点.
过A,F2两点.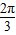 时,证明:点P在一定圆上;
时,证明:点P在一定圆上;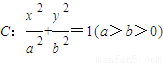 的左顶点为A,右焦点为F,且过点(1,
的左顶点为A,右焦点为F,且过点(1, ),椭圆C的焦点与曲线
),椭圆C的焦点与曲线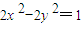 的焦点重合.
的焦点重合.