Question

【题目】已知动圆过定点，且内切于定圆．

（Ⅰ）求动圆圆心的轨迹方程；

（Ⅱ）在（Ⅰ）的条件下，记轨迹被所截得的弦长为，求的解析式及其最大值．

Answer 1

【答案】（Ⅰ）点的轨迹是以、为两焦点，长半轴为3的椭圆，方程为；（Ⅱ）．

【解析】

试题分析：（Ⅰ）根据题意设动圆的半径为，则，又动圆内切于定圆，所以有，所以，即，又，所以点轨迹是以为焦点，长轴长为的椭圆，，，所以，所以轨迹方程为；（Ⅱ）联立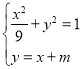，消去未知数得：，，解得，所以，设直线与椭圆交于两点，，，则弦长，所以有，当时，取得最大值．

试题解析：（Ⅰ）设动圆圆心，动圆半径为， ，

则，且，则,2分

即动圆圆心到两定点和的距离之和恰好等于定圆半径6，

又，，

所以点的轨迹是以、为两焦点，长半轴为3的椭圆．4分

则，故求点的轨迹方程为：．6分

（Ⅱ）联立方程组，消去，整理得5分

设交点坐标为，

则，解得，解得 6分

且7分

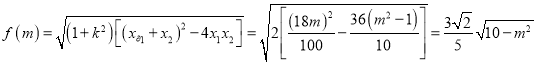故10分

当时，弦长取得最大值为．12分